
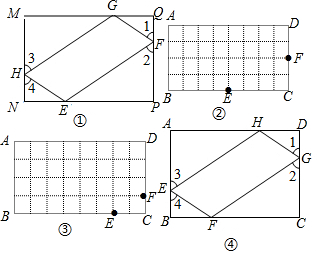
分析 (1)根据反射四边形的定义即可得;
(2)利用勾股定理分别求得各边的长度,由周长公式求解可得.
(3)延长HE交CB的延长线于N,延长HG交BC的延长线于M.作HK⊥BC于K.由△GCF≌△GCM,可得GF=GM,FC=CM,同理:EF=EN,BF=BN,想办法求出HM即可解决问题;
解答 解:(1)如图所示,四边形EFGH即为所求;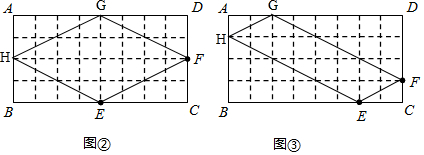
(2)在图②中,EF=FG=GH=HE=$\sqrt{{2}^{2}+{4}^{2}}$=2 $\sqrt{5}$,
∴反射四边形EFGH的周长为8 $\sqrt{5}$;
在图③中,EF=GH=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,HE=GF=$\sqrt{{3}^{2}+{6}^{2}}$=3 $\sqrt{5}$,
∴反射四边形EFGH的周长为2×$\sqrt{5}$+2×3 $\sqrt{5}$=8 $\sqrt{5}$.
猜想:矩形ABCD的反射四边形的周长是定值,定值为8$\sqrt{5}$.
(3)延长HE交CB的延长线于N,延长HG交BC的延长线于M.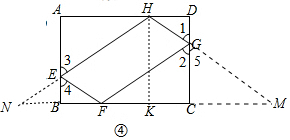
∵∠1=∠2=∠5,GC=GC,∠GCF=∠GCM=90°
∴△GCF≌△GCM,
∴GF=GM,FC=CM,
同理:EF=EN,BF=BN,
∴MN=2BC=16,
∵∠M=90°-∠5=90°-∠1,∠N=90°-∠3,∠1=∠3,
∴∠M=∠N,
∴HM=HN,
过点H作HK⊥BC于K.则HK=AB=4,KM=$\frac{1}{2}$MN=8,
∴HM=HN=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴四边形EFGH的周长=EF+FG+HG+EH=EN+EH+GH+HM=HN+HM=8$\sqrt{5}$.
点评 本题考查了应用与设计作图,全等三角形的判定与性质,勾股定理的应用,矩形的性质,读懂题意理解“反射四边形EFGH”特征是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.
图①是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
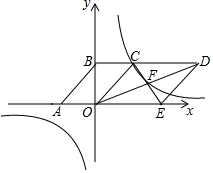 如图,已知反比例函数y=$\frac{1-m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,且经过?ABCO的顶点C,点A,B的坐标分别为(-2,0),(0,3),若点P是该反比例函数图象上的一点,且OC=OP,则满足条件的位于第三象限内P点坐标为(-3,-2)或(-2,-3);若该反比例函数图象又经过?COED对角线的交点F,则?COED的面积为18.
如图,已知反比例函数y=$\frac{1-m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,且经过?ABCO的顶点C,点A,B的坐标分别为(-2,0),(0,3),若点P是该反比例函数图象上的一点,且OC=OP,则满足条件的位于第三象限内P点坐标为(-3,-2)或(-2,-3);若该反比例函数图象又经过?COED对角线的交点F,则?COED的面积为18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
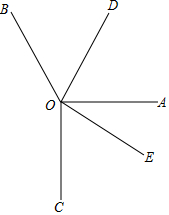 如图,∠AOB=120°,射线OD是∠AOB的角平分线,点C是∠AOB外部一点,且∠AOC=90°,点E是∠AOC内部一点,满足∠AOC=3∠AOE.
如图,∠AOB=120°,射线OD是∠AOB的角平分线,点C是∠AOB外部一点,且∠AOC=90°,点E是∠AOC内部一点,满足∠AOC=3∠AOE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AD=BC | B. | AC=BD | C. | BC∥AD | D. | ∠A=∠B |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,三角形ABC的三个顶点分别为A(-1,3)B(-4,1)C(-4,2)
如图,在直角坐标系中,三角形ABC的三个顶点分别为A(-1,3)B(-4,1)C(-4,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com