
【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为 ;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字与十位数字之和为8,且千位数字a使得二次函数y=(a﹣2)x2﹣(2a﹣3)x+a﹣3与x轴有两个交点,求出所有满足条件的“平衡数”M的值.
【答案】(1)1001;5261;(2)满足条件的“平衡数”M的值为3719.
【解析】
(1)根据平衡数的定义即可得解;
(2)根据平衡数的定义可知t=a+4,再由二次函数的性质得到a的取值范围,进而得到a的值,即可求得M的值.
(1)最小的“平衡数”为1001;
∴最大的“平衡数”为9999,
∴A=![]() ;
;
(2)设百位数字为t,则十位数字为8﹣t,
∵一个四位“平衡数”M的个位数字为3a,千位数字为a,
∴![]() ,解得t=a+4,
,解得t=a+4,
即一个四位“平衡数”M,它的千位数字围为a,百位数字为a+4,十位数字为4-a,个位数字为3a,
∵二次函数![]() 与x轴有两个交点,
与x轴有两个交点,
∴![]() 且
且![]() ,解得
,解得![]() 且a≠2,
且a≠2,
∴a=3,
∴满足条件的“平衡数”M的值为3719.


科目:初中数学 来源: 题型:
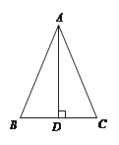
【题目】如图,△ABC中,AB=AC,过点A作AD⊥BC于点D.
(1)确定△ABC外接圆的圆心O,并画出△ABC的外接圆⊙O;(尺规作图,保留作图痕迹,不写作法)
(2)若BC=4,∠BAC=45°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),连接
重合),连接![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .作
.作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
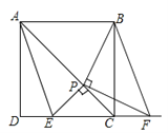
(1)由题意易知,![]() ,观察图,请猜想另外两组全等的三角形
,观察图,请猜想另外两组全等的三角形![]()
![]() ;
;![]()
![]() ;
;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)已知![]() ,
,![]() 的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于点A,交直线x=4于点B.
(1)抛物线的对称轴为x=____________(用含m的代数式表示)
(2)若AB∥x轴,求抛物线的解析式.
(3)记抛物线在A、B之间的部分为图象G(包含A、B两点),若对于图象G上任意一点P(xp,yp),都有yp≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.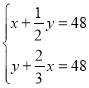 B.
B.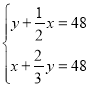 C.
C.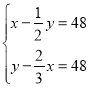 D.
D.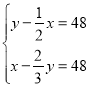
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级400名学生读书情况,随机调查了七年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数;
(2)根据样本数据,估计该校七年级400名学生在本次活动中读书多于3册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是把一个抛物线形桥拱,量得两个数据,画在纸上的情形.小明说只要建立适当的坐标系,就能求出此抛物线的表达式.你认为他的说法正确吗?如果不正确,请说明理由;如果正确,请你帮小明求出该抛物线的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
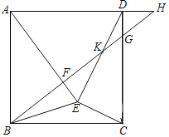
【题目】如图,在边长为4正方形ABCD中,以AB为腰向正方形内部作等腰△ABE,点G在CD上,且CG=3DG.连接BG并延长,与AE交于点F,与AD延长线交于点H.连接DE交BH于点K.若AE2=BFBH,则S△CDE=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com