
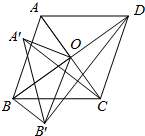
 已知:菱形ABCD的对角线AC,BD相交于点O,将△AOB绕点O逆时针方向旋转得到△A′OB′,旋转角为α(0°<α<90°),连接A′C,B′D,B′B,且AC=6,AD=5.
已知:菱形ABCD的对角线AC,BD相交于点O,将△AOB绕点O逆时针方向旋转得到△A′OB′,旋转角为α(0°<α<90°),连接A′C,B′D,B′B,且AC=6,AD=5.分析 (1)由菱形的性质,得出AO,再由勾股定理,求出BD,
(2)先由菱形性质,得出∠AOB=∠COD=90°,再由旋转得出关系,判断出△A′OC∽△B′OD,即可;
(3)由△A′OC∽△B′OD,得出$\frac{BD}{A′C}=\frac{OD}{CO}$=$\frac{4}{3}$,再判断出△BB′D是直角三角形,由勾股定理计算即可.
解答 解: (1)∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO=AC=$\frac{1}{2}$×6=3,BD=2DO.
∴∠AOB=∠COD=90°.
在Rt△AOD中,由勾股定理,得 DO=$\sqrt{A{D}^{2}-A{O}^{2}}$=4.
∴BD=2DO=2×4=8.
(2)∵四边形ABCD是菱形,
∴OC=OA=$\frac{1}{2}$AC,OD=OB=$\frac{1}{2}$BD,AC⊥BD,
∴∠AOB=∠COD=90°.
∵△AOB绕点O按逆时针方向旋转得到△A′OB′,
∴O A′=OA=OC,OB′=OB=OD,∠A′OB′=∠AOB=∠COD,
∴$\frac{OA′}{OC}=\frac{OB′}{OC}$,∠A′OB′+∠B′OC=∠COD+∠B′OC,
∴∠A′OC=∠B′OD.
∴△A′OC∽△B′OD.
∴∠OA′C=∠OB′D.
∴∠OA′C+∠CA′B′+∠A′B′O=∠A′O B′=∠CA′B′+∠A′B′O+∠OB′D=90°
∴A′C⊥B′D.
(3)B′B2+(mA′C)2的值不随旋转角α的变化而变化.
由(2)知△A′OC∽△B′OD,
∴$\frac{BD}{A′C}=\frac{OD}{CO}$=$\frac{4}{3}$,
∴B′D=A′C.
由(2)知OB=O B′=OD,
∴∠OB′B=∠OBB′,∠OB′D=∠ODB′,
∵∠OB′B+∠OBB′+∠OB′D+∠ODB′=180°,
∴∠OB′B+∠OB′D=90°.
∴△BB′D是直角三角形.
由勾股定理得 B′B2+B′D2=BD2=82=64
∴B′B2+( A′C)2=64.
∴B′B2+(mA′C)2的值不随旋转角α的变化而变化,其值为64.
点评 此题是四边形综合题,主要考查了直角三角形的判定和性质.相似三角形的性质和判定,菱形的性质和旋转的性质,判断出△A′OC∽△B′OD是解本题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
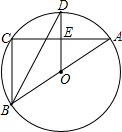 如图,AB是△ABC的外接圆⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,BC=5,AE=6,则DE的长为( )
如图,AB是△ABC的外接圆⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,BC=5,AE=6,则DE的长为( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )| A. | 上,下 | B. | 右,后 | C. | 左,右 | D. | 左,后 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
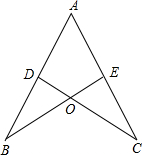 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com