Question

19．如图1，在平面直角坐标系中，直线y=x+4与x轴、y轴分别交于A、B两点，抛物线y=-x²+bx+c经过A、B两点，并与x轴交于另一点C（点C点A的右侧），点P是抛物线上一动点．
（1）求抛物线的解析式及点C的坐标；
（2）若点P在第二象限内抛物线上一点，过点P作PD∥y轴交AB于D，点E为线段DB上一点，且DE=2$\sqrt{2}$，过E做EF∥PD交抛物线于点F，当点P运动到什么位置时，四边形PDEF的面积最大？并求出此时点P的坐标；
（3）如图2，点F为AO的中点，连接BF，点G为y轴负半轴上一点且GO=2，沿x轴向右平移直线AG，记平移过程直线为A′G′，直线A′G′交x轴于点M，交直线AB为N，当△FMN为等腰三角形时，求平移后M点的坐标．

Answer 1

分析 （1）由直线方程可求得A、B两点的坐标，代入抛物线解析式可求得b、c的值，可求得抛物线解析式，再令y=0可求得C点坐标；
（2）过E作EH⊥PD于H，可求得EH，设出P点坐标，则可表示出D、E、F的坐标，从而可表示出PD和EF，利用梯形面积公式可表示出四边形PDEF的面积，根据二次函数的最值，可求得P点坐标；
（3）可求得直线AG和A′G′的方程，从而可表示出M、N点的坐标，从而可表示出MN、FM、FN的长，分MN=FM、MN=FN和FM=FN三种情况分别求解即可．

解答 解：
（1）∵直线y=x+4与x轴、y轴分别交于A、B两点，
∴A（-4，0），B（0，4），
∵抛物线y=-x²+bx+c经过A、B两点，
∴把A、B坐标代入可得$\left\{\begin{array}{l}{-16-4b+c=0}\\{c=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{b=-3}\\{c=4}\end{array}\right.$，
∴抛物线的解析式为y=-x²-3x+4，
令y=0可得：-x²-3x+4=0，解得x=1或x=-4，
∴C点坐标为（1，0）；
（2）如图，过E作EH⊥PD于H，则EH∥OA，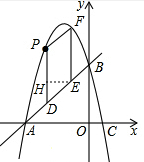

∵OA=OB=4，
∴∠OAB=45°，
∴∠HDE=45°，且DE=2$\sqrt{2}$，
∴HE=HD=2，
设P点坐标为（a，-a²-3a+4），
则D为（a，a+4），E为（a+2，a+6），F为（a+2，-a²-7a-6），
∴|PD|=-a²-3a+4-（a+4）=-a²-4a，|EF|=-a²-7a-6-（a+6）=-a²-8a-12，
∴S_{四边形PDEF}=$\frac{1}{2}$HE•（PD+EF）
=$\frac{1}{2}$×2（-a²-4a-a²-8a-12）
=-2a²-12a-12
=-2（a+3）²+6，
∴当a=-3时，S_{四边形PDEF}有最大值6，
此时P点坐标为（-3，4）；
（3）∵OG=2，
∴G点坐标为（0，2），且A（-4，0），
设直线AG方程为y=kx+n，把A、G坐标代入可得$\left\{\begin{array}{l}{-4k+n=0}\\{n=-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{n=-2}\end{array}\right.$，
∴直线AG方程为y=-$\frac{1}{2}$x-2，
∴可设直线A′G′的方程为y=-$\frac{1}{2}$（x-m）-2=-$\frac{1}{2}$x+$\frac{1}{2}$m-2，
令y=0可得=-$\frac{1}{2}$x+$\frac{1}{2}$m-2=0，解得x=m-4，
∴M点坐标为（m-4，0），
联立直线A′G′与直线AB方程可得$\left\{\begin{array}{l}{y=x+4}\\{y=-\frac{1}{2}x+\frac{1}{2}m-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=\frac{m-12}{3}}\\{y=\frac{m}{3}}\end{array}\right.$，
∴N点坐标为（$\frac{m-12}{3}$，$\frac{m}{3}$），
∵F为OA中点，
∴OF=2，即F（-2，0），
∴MF²=（m-4+2）²=m²-4m+4，
MN²=（m-4-$\frac{m-12}{3}$）²+（$\frac{m}{3}$-0）²=（$\frac{2}{3}$m）²+（$\frac{1}{3}$m）²=$\frac{5}{9}$m²，
NF²=（$\frac{m-12}{3}$+2）²+（$\frac{1}{3}$m）²=$\frac{2{m}^{2}-12m+36}{9}$，
当△FMN为等腰三角形时，分以下三种情况讨论：
①当MN=MF时，即$\frac{5}{9}$m²=m²-4m+4，
解得m=$\frac{9+3\sqrt{5}}{2}$或m=$\frac{9-3\sqrt{5}}{2}$，
此时M的坐标为（$\frac{1+3\sqrt{5}}{2}$，0）或（$\frac{1-3\sqrt{5}}{2}$，0）；
②当MN=NF时，即$\frac{5}{9}$m²=$\frac{2{m}^{2}-12m+36}{9}$，
解得m=-6或m=2，
此时M坐标为（-10，0）或M（-2，0）（与F点重合，舍去）；
③当MF=NF时，即m²-4m+4=$\frac{2{m}^{2}-12m+36}{9}$，
解得m=0或m=$\frac{24}{7}$，
此时M坐标为（-$\frac{4}{7}$，0）或（-4，0）（与A点重合，舍去）；
综上可知，平移后M点的坐标为（$\frac{1+3\sqrt{5}}{2}$，0）或（$\frac{1-3\sqrt{5}}{2}$，0）或（-$\frac{4}{7}$，0）．

点评 本题为二次函数的综合，涉及知识点有待定系数法、四边形的面积、二次函数的最值、平移、勾股定理及分类讨论思想．在（1）中求得A、B坐标是解题的关键，在（2）中用P点的坐标表示出四边形PDEF的面积是解题的关键，在（3）中分别表示出MF、NF、MN的长是解题的关键．本题考查知识点多，综合性强，计算量大，难度较大．