
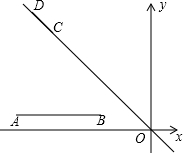
 已知线段AB,且A(-8,1)、B(-3,1),另有一线段CD在直线y=-x上,且CD=$\sqrt{2}$,确定D点位置,使A、B、C、D构成的四边形周长最短,并求D点坐标及这个最小值.
已知线段AB,且A(-8,1)、B(-3,1),另有一线段CD在直线y=-x上,且CD=$\sqrt{2}$,确定D点位置,使A、B、C、D构成的四边形周长最短,并求D点坐标及这个最小值. 分析 过点B作BE∥DC,取BE=$\sqrt{2}$,则BE=DC,作点E关于y=-x的对称点E′,连接E′A交y=-x于点D,首先可证明四边形DCBE为平行四边形,从而得到BE=DE,然后再求得点E的坐标,根据点E′与点E对称可知得到E′的坐标,从而可求得点AE的长度,进而可求得四边形周长的最小值,再求得直线AE′的解析式,然后再求得两直线交点的坐标即可.
解答 解:过点B作BE∥DC,取BE=$\sqrt{2}$,则BE=DC,作点E关于y=-x的对称点E′,连接E′A交y=-x于点D.
∵BE∥CD,BE=DC,
∴四边形DCBE为平行四边形.
∴ED=BC.
∵BE=$\sqrt{2}$,
∴EF=1,BF=1.
∵点B的坐标为(-3,1),
∴点E的坐标为(-4,2).
∵点E′与点E关于y=-x对称,
∴点E′的坐标为(-2,4).
设直线AE′的解析式为y=kx+b,根据题意得:$\left\{\begin{array}{l}{-2k+b=4}\\{-8k+b=1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=5}\end{array}\right.$
∴直线AE′的解析式为y=$\frac{1}{2}x+5$
将y=-x与y=$\frac{1}{2}x+5$组成方程组得:$\left\{\begin{array}{l}{y=-x}\\{y=\frac{1}{2}x+5}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=-\frac{10}{3}}\\{y=\frac{10}{3}}\end{array}\right.$,
∴点D的坐标为(-$\frac{10}{3}$,$\frac{10}{3}$).
根据两点间的距离公式得:AE′=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$
∴四边形周长得最小值=AB+DC+AE′=5+$\sqrt{2}$+3$\sqrt{5}$.
点评 本题主要考查的是轴对称-路径最短问题,掌握找出四边形周长最短满足的条件是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
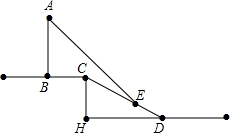 如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.
如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图:
某校初一数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图:| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | b |
| 占调查总人数的百分比 | 4% | 16% | m | 32% | n | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com