Question

(满分l2分)学完“等边三角形”这一节后，老师布置了一道思考题：
如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．
求证：∠BQM=60°．
(1)请你完成这道思考题；
(2)做完(1)后，同学们在老师的启发下进行了反思，提出了许多问题，如：
①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题?
②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM=60°?
③若将题中的条件“点M，N分别在正三角形ABC的BC，CA边上”改为“点M，N分别在正方形ABCD的BC，CD边上”，是否仍能得到∠BQM=60°?
请你作出判断，在下列横线上填写“是”或“否”：①______；②______；③______．并对②，③的判断，选择一个给出证明．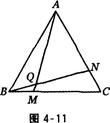

Answer 1

(1)证明：∵BM=CN，∠ABM=∠BCN，AB=BC．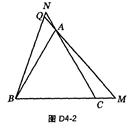


∴△ABM≌△BCN．∴∠BAM=∠CBN．
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=60°            ……4分
(2)①是；②是；③否．                           ……7分
②的证明：如图D4-2，
∵∠ACM=∠BAN=120°，CM=AN，AC=AB，
∴△ACM≌△BAN．∴∠AMC=∠BNA．
∴∠NQA=∠NBC+∠BMQ∴∠NBC+∠BNA=180°-60°=l20°．
∴∠BQM=60°．
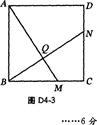
③的证明：如图D4—3，
∵BM=CN，AB=BC，
∴Rt△ABM≌Rt△BCN．
∴∠AMB=∠BNC．又∠NBM+∠BNC=90°，
∴∠QBM+∠QMB=90°．
∴∠BQM=90°，即∠BQM≠60°．                   ……l2分

解析