
【题目】已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() (如图①).
(如图①).

(1)求证:![]() ≌
≌![]() ;
;
(2)已知点![]() 是
是![]() 的中点,连接
的中点,连接![]() (如图②).
(如图②).
①求证:![]() ≌
≌![]() ;
;
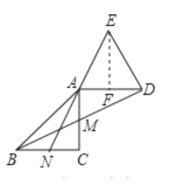
②如图③,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;
(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC即可得证;
②过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,得∠NAC=∠AEF,由(1)可知
,得∠NAC=∠AEF,由(1)可知![]() ,
,![]() 则可证
则可证![]() ,可证
,可证![]() ≌
≌![]() ,据此知
,据此知![]() ,再证
,再证![]() ,又
,又![]() 得
得![]() ,又因为
,又因为![]() ,从而得
,从而得![]() ,即可得证.
,即可得证.
(1)∵![]() 是
是![]() 中点
中点
∴![]()
又∵![]()
![]()
∴在![]() 与
与![]() 中
中
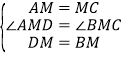
∴![]() ≌
≌![]() (
(![]() )
)
(2)① ![]()
![]() 是等腰直角三角形
是等腰直角三角形
∴ ![]()
∵ ![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点
中点
∴ ![]() ,
,![]()
∴ ![]()
又∵![]()
∴在![]() 与
与![]() 中
中

∴![]() ≌
≌![]() (
(![]() )
)
② 过点![]() 作
作![]() 交
交![]() 于点
于点![]()
∵ ![]()
∴ ![]()
由(1)可知![]() ≌
≌![]()
∴ ![]() ,
,![]()
∴ ![]()
∴ ![]()
在![]() 和
和![]() 中
中
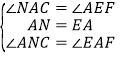
∴ ![]() ≌
≌![]() (
(![]() )
)
∴ ![]() ,
,![]() ,
,![]()
∵ ![]() 为
为![]() 中点
中点
∴ ![]() 为
为![]() 中点
中点
∴ ![]() 垂直平分
垂直平分![]()
∴ ![]()
∴ ![]()
∵ ![]()
∴ ![]()
∵ ![]()
∴ ![]()
即![]()
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,BC=10,tan∠ABC=![]() ,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
(1)当AE∥BC(如图(1))时,求⊙O的半径;
(2)设BO=x,AE=y,求y关于x的函数关系式;
(3)若以A为圆心的⊙A与⊙O有公共点D、E,当恰好也过点C时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A.点B同时出发,沿三角形的边运动,已知点M的速度为2cm/s,点N的速度为3cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动 秒后,△AMN是等边三角形?
(2)点M、N在BC边上运动时,运动 秒后得到以MN为底边的等腰三角形△AMN?
(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
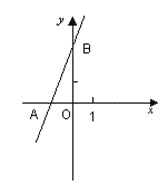
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“双十二购物狂欢节”活动,某零食店推出了甲、乙、丙三类饼干礼包,已知甲、乙、丙三类礼包均由![]() 、
、![]() 、
、![]() 三种饼干搭配而成,每袋礼包的成本均为
三种饼干搭配而成,每袋礼包的成本均为![]() 、
、![]() 、
、![]() 三种饼干成本之和.每袋甲类礼包有5包
三种饼干成本之和.每袋甲类礼包有5包![]() 种饼干、2包
种饼干、2包![]() 种饼干、8包
种饼干、8包![]() 种饼干;每袋丙类礼包有7包
种饼干;每袋丙类礼包有7包![]() 种饼干、1包
种饼干、1包![]() 种饼干、4包
种饼干、4包![]() 种饼干.已知甲每袋成本是该袋中
种饼干.已知甲每袋成本是该袋中![]() 种饼干成本的3倍,利润率为
种饼干成本的3倍,利润率为![]() ,每袋乙的成本是其售价的
,每袋乙的成本是其售价的![]() ,利润是每袋甲利润的
,利润是每袋甲利润的![]() ;每袋丙礼包利润率为
;每袋丙礼包利润率为![]() .若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为
.若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为![]() ,则当天该网店销售总利润率为__________.
,则当天该网店销售总利润率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com