
【题目】如图(1)所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示.已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出最长线段的长度?这样的线段可画几条?
(2)试比较立体图中![]() 与平面展开图中
与平面展开图中![]() 的大小关系?
的大小关系?

【答案】(1)![]() ,4条(2)相等
,4条(2)相等
【解析】解:(1)在平面展开图中可画出最长的线段长为![]() .
.
··········································1分
如图(1)中的![]() ,在
,在![]() 中
中
![]() ,由勾股定理得:
,由勾股定理得:
![]() ··········································3分
··········································3分
答:这样的线段可画4条(另三条用虚线标出).······4分
(2)![]() 立体图中
立体图中![]() 为平面等腰直角三角形的一锐角,
为平面等腰直角三角形的一锐角,
![]() .········································5分
.········································5分
在平面展开图中,连接线段![]() ,由勾股定理可得:
,由勾股定理可得:
![]() .········································7分
.········································7分
又![]() ,
,
由勾股定理的逆定理可得![]() 为直角三角形.
为直角三角形.
又![]() ,
,
![]() 为等腰直角三角形.···························8分
为等腰直角三角形.···························8分
![]() .········································9分
.········································9分
所以![]() 与
与![]() 相等.10分
相等.10分

(1)利用勾股定理求得在平面展开图中可画出最长的线段长为![]() ,由图可知这样的线段可画4条
,由图可知这样的线段可画4条
(2)立体图中![]() 为平面等腰直角三角形的一锐角,是
为平面等腰直角三角形的一锐角,是![]() ,在平面展开图中,连接线段
,在平面展开图中,连接线段![]() ,由勾股定理可得,
,由勾股定理可得,![]() ,由勾股定理的逆定理可得
,由勾股定理的逆定理可得![]() 为直角三角形,又
为直角三角形,又![]() ,得
,得![]() , 即可得出
, 即可得出![]() 与
与![]() 相等
相等


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明所在学校的旗杆BD高约为13米,距离旗杆20米处刚好有一棵高约为3米的香樟树AE.活动课上,小明有意在旗杆与香樟树之间的连线上来回踱步,发现有一个位置到旗杆顶部与树顶的距离相等.请你求出该位置与旗杆之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次科技活动中,小明进行了模拟雷达扫描实验.如图,表盘是△ABC,其中AB=AC,∠BAC=120°,在点A处有一束红外光线AP,从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.小明通过实验发现,光线从AB处旋转开始计时,旋转1秒,此时光线AP交BC边于点M,BM的长为(20 ![]() ﹣20)cm.
﹣20)cm. 
(1)求AB的长;
(2)从AB处旋转开始计时,若旋转6秒,此时光线AP与BC边的交点在什么位置?若旋转2014秒,交点又在什么位置?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( ) 
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“六一”儿童节的到来,某校学生参加献爱心捐款活动,随机抽取该校部分学生的捐款数进行统计分析,相应数据的统计图如下: 
(1)该样本的容量是 , 样本中捐款15元的学生有人;
(2)若该校一共有500名学生,据此样本估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动:探究利用角的对称性构造全等三角形解决问题
(1)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形;(写出简单做法,不用证明两三角形全等,不用尺规作图亦可)
(2)如图②,在△ABC中,∠ACB=90°,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请直接填空:∠AFE= 度,DF EF(填>,<或=);
(3)如图③,在△ABC中,如果∠ACB≠90°,而(2)中的其他条件不变,请问,你在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
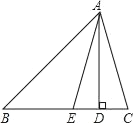
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线.
(1)若∠B=38°,∠C=70°,求∠DAE的度数;
(2)若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com