
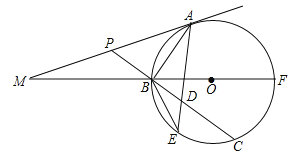
【题目】如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.
(1)求证:![]() ;
;
(2)若ED、EA的长是一元二次方程![]() 的两根,求BE的长;
的两根,求BE的长;
(3)若MA=![]() ,sin∠AMF=
,sin∠AMF=![]() ,求AB的长.
,求AB的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)连接OA、OE交BC于T.想办法证明OE⊥BC即可;
(2)由ED、EA的长是一元二次方程![]() 的两根,可得EDEA=5,由△BED∽△AEB,可得
的两根,可得EDEA=5,由△BED∽△AEB,可得![]() ,推出BE2=DEEA=5,即可解决问题;
,推出BE2=DEEA=5,即可解决问题;
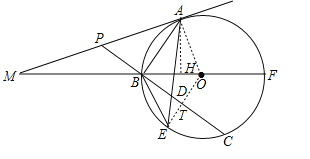
(3)作AH⊥OM于H.求出AH、BH即可解决问题;
试题解析:(1)证明:连接OA、OE交BC于T.
∵AM是切线,∴∠OAM=90°,∴∠PAD+∠OAE=90°,∵PA=PD,∴∠PAD=∠PDA=∠EDT,∵OA=OE,∴∠OAE=∠OEA,∴∠EDT+∠OEA=90°,∴∠DTE=90°,∴OE⊥BC,∴![]() .
.
(2)∵ED、EA的长是一元二次方程![]() 的两根,∴EDEA=5,∵
的两根,∴EDEA=5,∵![]() ,∴∠BAE=∠EBD,∵∠BED=∠AEB,∴△BED∽△AEB,∴
,∴∠BAE=∠EBD,∵∠BED=∠AEB,∴△BED∽△AEB,∴![]() ,∴BE2=DEEA=5,∴BE=
,∴BE2=DEEA=5,∴BE=![]() .
.
(3)作AH⊥OM于H.在Rt△AMO中,∵AM=![]() ,sin∠M=
,sin∠M=![]() =
=![]() ,设OA=m,OM=3m,∴9m2﹣m2=72,∴m=3,∴OA=3,OM=9,易知∠OAH=∠M,∴tan∠OAD=
,设OA=m,OM=3m,∴9m2﹣m2=72,∴m=3,∴OA=3,OM=9,易知∠OAH=∠M,∴tan∠OAD=![]() =
=![]() ,∴OH=1,AH=
,∴OH=1,AH=![]() .BH=2,∴AB=
.BH=2,∴AB=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
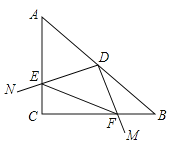
【题目】如图,在Rt△ABC 中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转分别交AC于点E,交BC于点F,则下列说法:①AE="CF" ②EC+CF=![]() ③DE="DF" ④若△ECF的面积为一个定值,则EF的长也是一个定值,其中正确的是( )
③DE="DF" ④若△ECF的面积为一个定值,则EF的长也是一个定值,其中正确的是( )
A.①②B.①③C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金![]() 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同,![]() 值应是多少?此时,哪种方案对公司更有利?
值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=![]() ,点D为AC与反比例函数
,点D为AC与反比例函数![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1) 若确定甲打第一场,再从其余三位同学中随机选取一位,恰好选中乙同学的概率是 .
(2) 若随机抽取两位同学,请用画树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com