
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
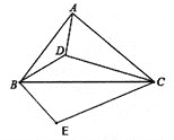
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
【答案】(1)90°;(2)①见解析;②![]()
【解析】
(1)根据三角形外角的性质进行解答即可;
(2)①根据两边成比例且夹角相等即可证明△ACD∽△BCE;
②先根据等腰直角三角形的性质得:![]() ,证明△ACB∽△DCE,得
,证明△ACB∽△DCE,得![]() ,代入所求的式子可得结论.
,代入所求的式子可得结论.
(1)解:如图1,延长CD交AB于F,

∵∠ADF=∠CAD+∠ACD,∠BDF=∠CBD+∠BCD,
∴∠ADB=∠ADF+∠BDF=∠CAD+∠CBD+∠ACB,
∵∠ADB=∠ACB+90°.
∴∠CAD+∠CBD=90°;
(2)①证明:如图2,∵∠CAD+∠CBD=90°,∠CBD+∠CBE=90°,
∴∠CAD=∠CBE,
∵ACBD=ADBC,BE=BD,
∴![]() ,
,
∴△ACD∽△BCE;
②解:如图2,连接DE,

∵BE⊥BD,BE=BD,
∴△BDE是等腰直角三角形,
∴![]()
∵△ACD∽△BCE,
∴∠ACD=∠BCE,![]() ,
,
∴∠ACB=∠DCE,
∴△ACB∽△DCE,
∴![]() ,
,
∴![]()


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】(2017宁夏)在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
(1)求证:不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)当BP的长为何值时,四边形AMPN的面积最大,并求出最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆周上一点,连接AC、BC,以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P,使∠1=∠2=∠A.

(1)求证:直线PC是⊙O的切线;
(2)若CD=4,BD=2,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() 的图象相交于点A,并与
的图象相交于点A,并与![]() 轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
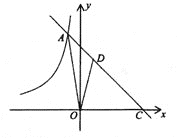
(1)求![]() 的值;
的值;
(2)求点D的坐标;
(3)根据图象,直接写出当![]() 时不等式
时不等式![]() 的
的![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是边长为2的正方形ABCD的边BC上的一动点(不与端点重合),将△ABE沿AE翻折至△AFE的位置,若△CDF是等腰三角形,则BE=________.
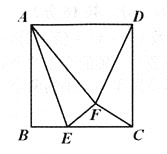
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.
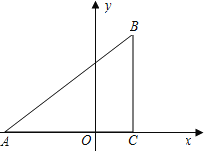
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店的员工与老板齐心协力,在2019年的经营中,每月的利润都在不断增加.该服装店的老板每季度都让员工总结经验与不足,下面是策划师与销售![]() 品牌服装的员工在第二季度总结的一部分.
品牌服装的员工在第二季度总结的一部分.
策划师的发言:第四月的利润为50万元,从第四月开始,第二季度的月增长率不变,第二季度的总利润为182万元.
销售![]() 品牌的员工发言:销售的
品牌的员工发言:销售的![]() 品牌服装在四月份中,进价为100元,售价为140元,每周销售60件,由于该服装进货量少,因此,采用涨价销售,每件涨1元时,平均每周少售2件,每周盈利2250元.
品牌服装在四月份中,进价为100元,售价为140元,每周销售60件,由于该服装进货量少,因此,采用涨价销售,每件涨1元时,平均每周少售2件,每周盈利2250元.

请根据总结解答相关的问题:
(1)求第二季度月增长率;
(2)![]() 品牌服装每周盈利2250元时,每件售价应该是多少元?
品牌服装每周盈利2250元时,每件售价应该是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A. ((k﹣1)n,0) B. ((k+![]() )n,0)) C. (
)n,0)) C. (![]() ,0) D. ((k+1)n,0)
,0) D. ((k+1)n,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,m),Q(1,n)在二次函数y=(x+a)(x﹣a﹣1)(a≠0)的图象上,且m<n下列结论:①该二次函数与x轴交于点(﹣a,0)和(a+1,0);②该二次函数的对称轴是x=![]() ; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com