
【题目】已知关于x的一元二次方程x2-(2k+3)+k2+3k-4=0.
(1) 试判断上述方程根的情况并说明理由;
(2) 若以上一元二次方程的两个根分别为![]() 、
、![]() (
(![]() ),
),
① m=________,n=_________;
②当![]() 时,点A、B分别是直线
时,点A、B分别是直线![]() :y=kx+
:y=kx+![]() 上两点且A、B两点的横坐标分别为
上两点且A、B两点的横坐标分别为![]() 、
、![]() ,直线
,直线![]() 与
与![]() 轴相交于点C,若S△BOC=2S△AOC,求
轴相交于点C,若S△BOC=2S△AOC,求![]() 的值;
的值;
(3)在(2)的条件下,问在![]() 轴上是否存在点Q,使△ABQ的三个内角平分线交点在
轴上是否存在点Q,使△ABQ的三个内角平分线交点在![]() 轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
【答案】(1)方程有两个不相等的实数根,理由略;(2)①m=k-1 n=k+4;② k=![]() ;(3)(0,
;(3)(0,![]() ) .
) .
【解析】
(1)根据判别式的值即可判断;
(2)①根据一元二次方程的求根公式即可得出;
②先根据三角形的面积公式列出关于m,n的式子,再将m= k-1,n= k+4代入,即可得出答案;
(3)假设存在点Q,使△ABQ的三个内角平分线交点在![]() 轴上,则此时y轴就是∠AQB的角平分线,从而得知点B(
轴上,则此时y轴就是∠AQB的角平分线,从而得知点B(![]() ,5)和对称点B'(-
,5)和对称点B'(-![]() ,5)在直线AQ上,待定系数法可得直线AQ的解析式,由点Q在y轴上即可得点Q的坐标.
,5)在直线AQ上,待定系数法可得直线AQ的解析式,由点Q在y轴上即可得点Q的坐标.
解:(1)∵x2-(2k+3)x+k2+3k-4=0,
∴△=b2-4ac=(2k+3)2-4(k2+3k-4)=4k2+12k+9-4k2-12k+16=25>0,
∴该方程有两个不相等的实数根.
(2)①∵一元二次方程的求根公式x=![]() ,
,
∴m=![]() =
=![]() =
=![]() =k-1,
=k-1,
n=![]() =
=![]() =
=![]() =k+4.
=k+4.
② ∵S△BOC=2S△AOC,
S△BOC=![]() ×
×![]() ×(
×(![]() ),
),
S△AOC=![]() ×
×![]() ×(
×(![]() ),
),
∴![]() ×
×![]() ×(
×(![]() )×2=
)×2=![]() ×
×![]() ×(
×(![]() ),
),
∴2(![]() )=
)=![]() ,
,
2km-kn=-![]() ,
,
将m= k-1,n= k+4代入,得:2k(k-1)-k(k+4)+![]() =0,
=0,
解得:k=![]() 或
或![]() ,
,
∵0<k<1,
∴k=![]() .
.
(3)由(2)得知,直线l:![]() ,A(
,A(![]() ,
,![]() ),B(
),B(![]() ,5),
,5),
假设存在点Q,使△ABQ的三个内角平分线交点在![]() 轴上,则此时y轴就是∠AQB的角平分线,
轴上,则此时y轴就是∠AQB的角平分线,
∴B点关于y轴的对称点必在直线AQ上,设为B',
∵B(![]() ,5),
,5),
∴B'(-![]() ,5).
,5).
∴直线AQ过A(![]() ,
,![]() ),B'(-
),B'(-![]() ,5)得到AQ的直线方程为:
,5)得到AQ的直线方程为:![]() ,
,
∵点Q在y轴上,当x=0时,y=![]() ,
,
∴Q(0,![]() ).
).


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC 是边长为 4 的等边三角形,点 D 是 AB 上异 于 A,B 的一动点,将△ACD 绕点 C 逆时针旋转 60°得△BCE, 则旋转过程中△BDE 周长的最小值_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
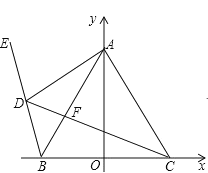
【题目】如图,已知 B 1, 0 , C 1, 0 , A 为 y 轴正半轴上一点, AB AC ,点 D 为第二象限一动点,E 在 BD 的延长线上, CD 交 AB 于 F ,且BDC BAC .
(1)求证: ABD ACD ;
(2)求证: AD 平分CDE ;
(3)若在 D 点运动的过程中,始终有 DC DA DB ,在此过程中,BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出BAC 的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程.
(1)2(1-x)2-8=0 (2 )2x2![]() x-1=0 (公式法)
x-1=0 (公式法)
(3)x2-3x+1=0(配方法) (4) (x-1)2-5(x-1)+6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.

(1)求证:AD是⊙O的切线;
(2)若⊙O的直径为6,线段BC=2,求∠BAC的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点(0,1),且与正比例函数y=![]() x的图象相交于点(2,a).
x的图象相交于点(2,a).

求:(1)a的值;
(2)一次函数y=kx+b的解析式;
(3)在图中画出这两个函数图象,并求这两个函数图象与x轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动。校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如下图所示:

根据以上信息,解答下列问题:
(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为 ;
(2)求本次所抽取学生四月份“读书量”的平均数;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com