
”¾ĢāÄæ”æĪŅŹŠÄ³ÖŠŃ§¼Ę»®¹ŗ½ųČōøÉøö¼×ÖÖ¹ęøńµÄÅÅĒņŗĶŅŅÖÖ¹ęøńµÄ×ćĒņ£® Čē¹ū¹ŗĀņ20øö¼×ÖÖ¹ęøńµÄÅÅĒņŗĶ15øöŅŅÖÖ¹ęøńµÄ×ćĒņ£¬Ņ»¹²ŠčŅŖ»Ø·Ń2050ŌŖ£» Čē¹ū¹ŗĀņ10øö¼×ÖÖ¹ęøńµÄÅÅĒņŗĶ20øöŅŅÖÖ¹ęøńµÄ×ćĒņ£¬Ņ»¹²ŠčŅŖ»Ø·Ń1900ŌŖ£®
£Ø1£©ĒóĆæøö¼×ÖÖ¹ęøńµÄÅÅĒņŗĶĆæøöŅŅÖÖ¹ęøńµÄ×ćĒņµÄ¼Ūøń·Ö±šŹĒ¶ąÉŁŌŖ?
£Ø2£©Čē¹ūѧŠ£ŅŖ¹ŗĀņ¼×ÖÖ¹ęøńµÄÅÅĒņŗĶŅŅÖÖ¹ęøńµÄ×ćĒņ¹²50øö£¬²¢ĒŅŌ¤Ėć×Ü·ŃÓĆ²»³¬¹ż3210ŌŖ£¬ÄĒĆ“øĆѧŠ£ÖĮ¶ąÄܹŗĀņ¶ąÉŁøöŅŅÖÖ¹ęøńµÄ×ćĒņ?
”¾“š°ø”æ£Ø1£©50,70£»£Ø2£©35£»
”¾½āĪö”æ
£Ø1£©¼×ŅŅ¹ęøńµÄĒņ¼Ūøń·Ö±šÉčĪŖx£¬y£¬øł¾ŻĢāŅāĮŠ³ö¶žŌŖŅ»“Ī·½³Ģ×飬¼“æÉĒó³ö½į¹ū£»
£Ø2£©ÉčĪ“ÖŖŹżx£¬øł¾ŻĢāŅāŅŌ¼°Ņ»ĪŹÖŠµÄ½į¹ūĮŠ³ö²»µČŹ½£¬½ā²»µČŹ½£¬Č”Õū£¬¼“ĪŖĖłĒó“š°ø£®
£Ø1£©ÉčĆæøö¼×ÖÖ¹ęøńµÄÅÅĒņµÄ¼ŪøńŹĒxŌŖ£¬ĆæøöŅŅÖÖ¹ęøńµÄ×ćĒņµÄ¼ŪøńŹĒyŌŖ£¬
øł¾ŻĢāŅāµĆ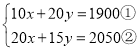 £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
“š£ŗĆæøö¼×ÖÖ¹ęøńµÄÅÅĒņµÄ¼ŪøńŹĒ50ŌŖ£¬ĆæøöŅŅÖÖ¹ęøńµÄ×ćĒņµÄ¼ŪøńŹĒ70ŌŖ£»
£Ø2£©ÉčøĆѧŠ£¹ŗĀņmøöŅŅÖÖ¹ęøńµÄ×ćĒņ£¬Ōņ¹ŗĀņ¼×ÖÖ¹ęøńµÄÅÅĒņ(50-m)øö£¬øł¾ŻĢāŅāµĆ³ö£ŗ50(50-m)+70m”Ü3210£¬½āµĆm”Ü35.5£»
“š£ŗøĆѧŠ£ÖĮ¶ąÄܹŗĀņ35øöŅŅÖÖ¹ęøńµÄ×ćĒņ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻACB=90”ć£¬”ĻB=55”ć£¬µćDŹĒŠ±±ßABµÄÖŠµć£¬ÄĒĆ“”ĻACDµÄ¶ČŹżĪŖ£Ø £©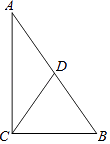
A.15”ć
B.25”ć
C.35”ć
D.45”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó¾¹żA£Ø©2£¬©1£©£¬B£Ø1£¬3£©Į½µć£¬²¢ĒŅ½»xÖįÓŚµćC£¬½»yÖįÓŚµćD£®
£Ø1£©ĒóøĆŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©Ēó”÷AOBµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ĻMON=30”ć£¬BĪŖOMÉĻŅ»µć£¬BA”ĶONÓŚA£¬ĖıߊĪABCDĪŖÕż·½ŠĪ£¬PĪŖÉäĻßBMÉĻŅ»¶Æµć£¬Į¬½įCP£¬½«CPČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ90”ćµĆCE£¬Į¬½įBE£¬ČōAB=4£¬ŌņBEµÄ×īŠ”ÖµĪŖ £® 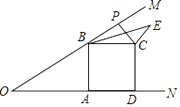
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌČĪŅāÓŠĄķŹżx£¬ÓĆ[x]±ķŹ¾²»“óÓŚxµÄ×ī“óÕūŹż£®ĄżČē£ŗ[1.3]£½1£¬[3]£½3£¬[©2.5]£½©3£®ŅŌĻĀ½įĀŪÕżČ·µÄŹĒ_____£®£Ø°ŃÄćČĻĪŖÕżČ·½įĀŪµÄŠņŗŶ¼ĢīÉĻ£©
¢Ł[©3.14]£½©4£»
¢Ś©[©x]£½[x]£»
¢Ū[2x]£½2[x]£»
¢ÜČō[![]() ]£½©4£¬ŌņxµÄȔֵ·¶Ī§ŹĒ©
]£½©4£¬ŌņxµÄȔֵ·¶Ī§ŹĒ©![]() ”Üx£¼©
”Üx£¼©![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬µćOŌŚACÉĻ£¬ŅŌOAĪŖ°ė¾¶µÄ”ŃO½»ABÓŚµćD£¬BDµÄ“¹Ö±Ę½·ÖĻß½»BCÓŚµćE£¬½»BDÓŚµćF£¬Į¬½ÓDE£®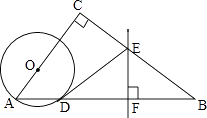
£Ø1£©ÅŠ¶ĻÖ±ĻßDEÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČōAC=6£¬BC=8£¬OA=2£¬ĒóĻ߶ĪDEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĶ¼ŠĪÖŠ£¬ŹĒÖį¶Ō³ĘĶ¼ŠĪµ«²»ŹĒÖŠŠÄ¶Ō³ĘĶ¼ŠĪµÄŹĒ£Ø £©
A.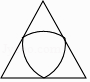
B.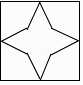
C.
D.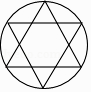
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ¹ÄĄųŹŠĆń½ŚŌ¼ÓĆĖ®£¬Ä³ŹŠ¾ÓĆńÉś»īÓĆĖ®°“½×ĢŻŹ½Ė®¼Ū¼Ę·Ń£®ĻĀ±ķŹĒøĆŹŠ¾ÓĆń»§Ņ»±ķÉś»īÓĆĖ®½×ĢŻŹ½¼Ę·Ń¼Ūøń±ķµÄ²æ·ÖŠÅĻ¢£ŗ
×ŌĄ“Ė®ĻśŹŪ¼Ūøń | ĪŪĖ®“¦Ąķ¼Ūøń | |
Ć滧ĆæŌĀÓĆĖ®Įæ | µ„¼Ū£ŗŌŖ/¶Ö | µ„¼Ū£ŗŌŖ/¶Ö |
|
|
|
³¬¹ż 17 ¶Öµ«²»³¬¹ż 30 ¶ÖµÄ²æ·Ö |
|
|
³¬¹ż 30 ¶ÖµÄ²æ·Ö |
|
|
ĖµĆ÷£ŗ¢ŁĆ滧²śÉśµÄĪŪĖ®ĮæµČÓŚøĆ»§×ŌĄ“Ė®ÓĆĖ®Į棻¢ŚĖ®·Ń=×ŌĄ“Ė®·ŃÓĆ£«ĪŪĖ®“¦Ąķ·Ń£®
£Ø1£©É芔Ķõ¼ŅŅ»øöŌĀµÄÓĆĖ®ĮæĪŖ![]() ¶Ö£¬ĖłÓ¦½»µÄĖ®·ŃĪŖ
¶Ö£¬ĖłÓ¦½»µÄĖ®·ŃĪŖ![]() ŌŖ£¬ĒėŠ“³ö
ŌŖ£¬ĒėŠ“³ö![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½£»
µÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©Ėę×ÅĻÄĢģµÄµ½Ą“£¬ÓĆĖ®Į潫Ōö¼Ó£®ĪŖĮĖ½ŚŹ”æŖÖ§£¬Š”Ķõ¼Ę»®°Ń7ŌĀ·ŻµÄĖ®·ŃæŲÖĘŌŚ²»³¬¹ż¼ŅĶ„ŌĀŹÕČėµÄ![]() .ČōŠ”Ķõ¼ŅµÄŌĀŹÕČėĪŖ
.ČōŠ”Ķõ¼ŅµÄŌĀŹÕČėĪŖ![]() ŌŖ£¬ŌņŠ”Ķõ¼Ņ7ŌĀ·Ż×ī¶ąÄÜÓƶąÉŁ¶ÖĖ®£æ
ŌŖ£¬ŌņŠ”Ķõ¼Ņ7ŌĀ·Ż×ī¶ąÄÜÓƶąÉŁ¶ÖĖ®£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬BCŹĒ”ŃOµÄÖ±¾¶£¬µćAŌŚ”ŃOÉĻ£¬AD”ĶBC£¬“¹×ćĪŖD£¬»”AEµČÓŚ»”AB£¬BE·Ö±š½»AD”¢ACÓŚµćF”¢G£® 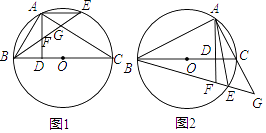
£Ø1£©ÅŠ¶Ļ”÷FAGµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČōµćEŗĶµćAŌŚBCµÄĮ½²ą£¬BE”¢ACµÄŃÓ³¤Ļß½»ÓŚµćG£¬ADµÄŃÓ³¤Ļß½»BEÓŚµćF£¬ĘäÓąĢõ¼ž²»±ä£¬£Ø1£©ÖŠµÄ½įĀŪ»¹³ÉĮ¢Āš£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com