【题目】已知AB是⊙O的直径，C是圆上的点，D是优弧ABC的中点．
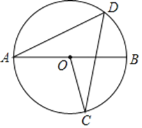
（1）若∠AOC＝100°，则∠D的度数为 ，∠A的度数为 ；
（2）求证：∠ADC＝2∠DAB．
科目：初中数学 来源： 题型：
【题目】如图，已知⊙O的半径是2，点A、B、C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（ ）
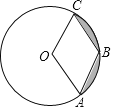
A. 
π﹣2
B. 
π﹣ C. 
π﹣2 D. π﹣
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球(有放回)，下表是活动进行中的一组统计数据。
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率mn | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
(1)补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是______；（保留小数点后两位）
(2)估算袋中白球的个数；
(3)在(2)的条件下，若小强同学有放回地连续两次摸球，用画树形图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝4cm，若以点C为圆心，以2cm为半径作⊙C，则AB与⊙C的位置关系是（ ）
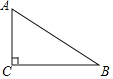
A.相离B.相切C.相交D.相切或相交
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB＝AC＝2
，∠BAC＝120°，D为BC边上的点，将DA绕D点逆时针旋转120°得到DE．
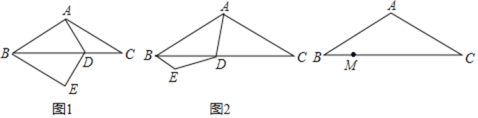
（1）如图1，若AD＝DC，则BE的长为 ，BE2+CD2与AD2的数量关系为 ；
（2）如图2，点D为BC边山任意一点，线段BE、CD、AD是否依然满足（1）中的关系，试证明；
（3）M为线段BC上的点，BM＝1，经过B、E、D三点的圆最小时，记D点为D1，当D点从D1处运动到M处时，E点经过的路径长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了深入学习社会主义核心价值观，对本校学生进行了一次相关知识的测试，随机抽取了部分学生的测试成绩进行统计（根据成绩分为
、
、
、
、
五个组，
表示测试成绩，组：
；组：
；组：
；组：
；组：
），通过对测试成绩的分析，得到如图所示的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
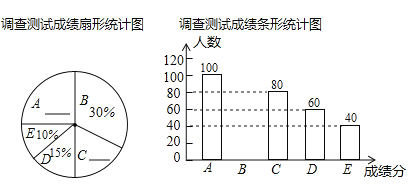
（1）抽取的学生共有______人，请将两幅统计图补充完整；
（2）抽取的测试成绩的中位数落在______组内；
（3）本次测试成绩在80分以上（含80分）为优秀，若该校初三学生共有1200人，请估计该校初三测试成绩为优秀的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等边△ABC中，AB＝12．以AB为直径的半⊙O与边AC相交于点D．过点D作DE⊥BC，垂足为E；过点E作EF⊥AB，垂足为F，连接DF．
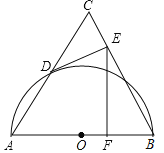
（1）求证：DE是⊙O的切线；
（2）求EF的长；
（3）求sin∠EFD的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
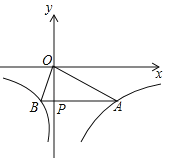
【题目】（2017四川省达州市，第10题，3分）已知函数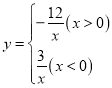
的图象如图所示，点P是y轴负半轴上一动点，过点P作y轴的垂线交图象于A，B两点，连接OA、OB．下列结论：
①若点M1（x1，y1），M2（x2，y2）在图象上，且x1＜x2＜0，则y1＜y2；
②当点P坐标为（0，﹣3）时，△AOB是等腰三角形；
③无论点P在什么位置，始终有S△AOB=7.5，AP=4BP；
④当点P移动到使∠AOB=90°时，点A的坐标为（
，
）．
其中正确的结论个数为（ ）
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
