
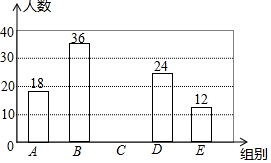
 为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:
为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:| 组别 | 平均每天完成家庭作业的时间(x分钟) | 频数(人数) | 频率 |
| A | x≤40 | 18 | 0.15 |
| B | 40<x≤60 | a | b |
| C | 60<x≤80 | ||
| D | 80<x≤100 | 24 | 0.20 |
| E | x>100 | 12 | 0.10 |
| 合计 | c | 1.00 | |
分析 (1)由A组频数及其频率可得总人数c,由条形图可得a=36,用B组频数÷总数可得b,根据频数之和等于总数求得C组人数,补全图形;
(2)根据中位数的定义求解可得;
(3)根据样本估计总体的思想方法解答可得.
解答 解:(1)∵本次调查的总人数c=18÷0.15=120(人),由条形图知a=36,
∴b=36÷120=0.2,
则C组人数为:120-(18+36+24+12)=30(人),
补全条形图如下: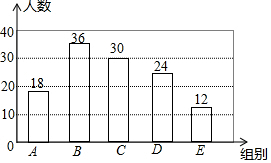
故答案为:36,0.3,120;
(2)120个数据的中位数为第60、61个数据的平均数,而第60、61个数均落在C组,
∴这次调查中,学生平均每天完成家庭作业时间的中位数出现在C组,
故答案为:C;
(3)①上述过程主要体现的数学思想是样本估计总体;
②不合理,应为该样本是七年级的学生中抽取的,对于八、九年级学生来说不具有代表性.
故答案为:样本估计总体.
点评 本题考查频数分布直方图、用样本估计总体、频数分布表,解题的关键是明确题意,找出所求问题需要的条件,会用样本估计总体.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
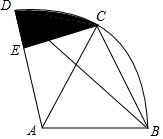 如图所示,在扇形BAD中,点C在$\widehat{BD}$上,且∠BDC=30°,AB=2$\sqrt{2}$,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
如图所示,在扇形BAD中,点C在$\widehat{BD}$上,且∠BDC=30°,AB=2$\sqrt{2}$,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )| A. | π-2 | B. | π-1 | C. | 2π-2 | D. | 2π+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
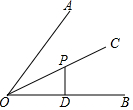 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
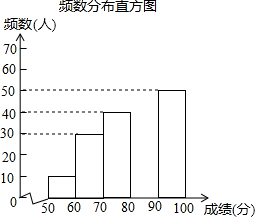 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:| 成绩x(分) | 频数(人) | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com