【答案】分析:由于a,b,c均为非零实数,且a+b+c=0,得到a,b,c中一定有正数与负数,然后讨论:当a,b,c中只有一个正数数时,设a>0,b<0,c<0;当a,b,c中有两个正数数时,设a>0,b>0,c<0,再分别根据绝对值的意义去绝对值、约分后计算即可.
解答:解:∵a+b+c=0,
∴a,b,c中一定有正数与负数,
当a,b,c中只有一个正数数时,设a>0,b<0,c<0,
∴原式=1×(-1)+(-1)×(-1)+(-1)×1=-1+1-1=-1;
当a,b,c中有两个正数数时,设a>0,b>0,c<0,
原式=1×1+1×(-1)+(-1)×1=1-1-1=-1.
故答案为-1.
点评:本题考查了分式的化简求值:利用绝对值的意义先去绝对值,然后约分即可.

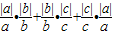 = .
= . 

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案