
 某校有一长方形花圃,里面有一些杂草需要处理.小聪单独完成这项杂草清除任务需要150分钟,小聪单独施工30分钟后,小明加入清理,两人又共同工作了15分钟,完成总清理任务的$\frac{1}{3}$.
某校有一长方形花圃,里面有一些杂草需要处理.小聪单独完成这项杂草清除任务需要150分钟,小聪单独施工30分钟后,小明加入清理,两人又共同工作了15分钟,完成总清理任务的$\frac{1}{3}$.分析 (1)设乙队单独完成这项工程需要x天,根据题意得方程即可得到结论;
(2)根据题意得:(km+m)×40=$\frac{2}{3}$,即可得到m=$\frac{1}{60(k+1)}$,根据反比例函数的性质得到k=1时,m取最大值,即可得到结论.
解答 解:(1)设小明单独完成这项清理任务需要x分钟,
根据题意得:$\frac{1}{150}$×(30+15)+$\frac{1}{x}$×15=$\frac{1}{3}$,
解得x=450,
经检验x=450是方程的根.
答:小明队单独完成这项清理任务需要450分钟.
(2)根据题意得:(km+m)×40=$\frac{2}{3}$,
解得m=$\frac{1}{60(k+1)}$,
当1≤k≤2时,m随k的增大而减小,
当k=1时,m最大值为$\frac{1}{120}$.
故答案为:$\frac{1}{120}$.
点评 此题考查了一次函数的实际应用.分式方程的应用,解题的关键是理解题意,能根据题意求得函数解析式,注意数形结合与方程思想的应用.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.312 | B. | $-\frac{1}{6}$ | C. | $\frac{π}{3}$ | D. | 1.$\stackrel{•}{2}$3$\stackrel{•}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
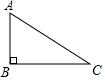 如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( )
如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( )| A. | 7个 | B. | 9个 | C. | 11个 | D. | 12个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
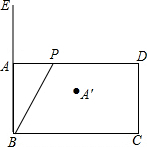 如图,矩形ABCD中,AB=2,BC=2$\sqrt{3}$,动点P从A点出发,沿AD运动到D点,连接BP,点A关于直线BP的对称点为A′,
如图,矩形ABCD中,AB=2,BC=2$\sqrt{3}$,动点P从A点出发,沿AD运动到D点,连接BP,点A关于直线BP的对称点为A′,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com