
| ����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
| ��������Ĵ���m | 58 | 96 | 116 | 295 | 484 | 601 |
| ���������Ƶ�� | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
���� ��1������ͳ�����ݣ���n�ܴ�ʱ�����������Ƶ�ʽӽ�0.6��
��2����������Ƶ�ʹ��Ƹ��ʣ��ɹ�����������ĸ���Ϊ0.6��Ȼ�����ø��ʹ�ʽ�������ĸ�����
��3���������б���չʾ����20�ֵȿ��ܵĽ���������ҳ���ֻ����ɫ��ͬ��ռ�������Ȼ����ݸ��ʹ�ʽ��⣮
��� �⣺��1����n�ܴ�ʱ�����������Ƶ�ʽ���ӽ�0.6��
�ʴ�Ϊ��0.6��
��2���ɣ�1����������ĸ���Ϊ0.6�����Կɹ��ƿڴ��а�����ɫ����ĸ����ǣ�5��0.6=3��ֻ����
��3���������⻭��״ͼ���£�
����20�ֵȿ��ܵĽ������������ֻ����ɫ��ͬռ8�֣�
������ֻ����ɫ��ͬ�ĸ���=$\frac{8}{20}$=$\frac{2}{5}$��
���� ���⿼��������Ƶ�ʹ��Ƹ��ʣ������ظ�ʵ��ʱ���¼�������Ƶ����ij���̶�λ�����Ұڶ������Ұڶ��ķ���Խ��ԽС���������Ƶ���ȶ��Զ�����������Ƶ�ʵļ������������Ƹ��ʣ�����̶��Ľ���ֵ��������¼��ĸ��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
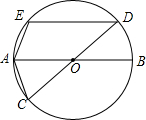 ��ͼ��AB��CD���ǡ�O��ֱ������DE��AB��
��ͼ��AB��CD���ǡ�O��ֱ������DE��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������һ�ֶ������ݱ�ֲ�Ϊ��ø������¶�����⣬�侥�������Ÿ��������������·���������ϣ���������ɿ���Բ���壬���ĵ����ܳ���50cm����һ�θ�������������2Ȧ����Ϊ2.4mʱ����θ��ٵij��ǣ�������m��
������һ�ֶ������ݱ�ֲ�Ϊ��ø������¶�����⣬�侥�������Ÿ��������������·���������ϣ���������ɿ���Բ���壬���ĵ����ܳ���50cm����һ�θ�������������2Ȧ����Ϊ2.4mʱ����θ��ٵij��ǣ�������m��| A�� | 3 | B�� | 2.6 | C�� | 2.8 | D�� | 2.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | 0.1 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2$\sqrt{2}$��m��2$\sqrt{2}$ | B�� | -2$\sqrt{2}$��m��2 | C�� | -2��m��2 | D�� | -2��m��2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com