
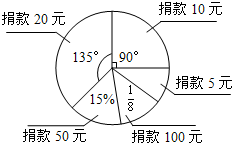
 在抗震救灾的捐款活动中,六(2)班同学的捐款人数情况如图所示,其中捐款10元的人数为10人.请根据图象回答下列问题:
在抗震救灾的捐款活动中,六(2)班同学的捐款人数情况如图所示,其中捐款10元的人数为10人.请根据图象回答下列问题:分析 (1)把六年级(2)班捐款的总人数看作单位“1”,(1)可计算出捐款10元所占的圆心角占整个圆心角的几分之几,然后用10除以所得到的分数就是六年级(2)班的捐款的总人数;
(2)用单位“1”减去捐款10元的圆心角占整个圆心角的分数再减去捐款20元的圆心角占整个圆心角的分数减去15%再减去$\frac{1}{8}$就是捐款5元的占捐款总人数的分数,最后再用捐款的总人数乘捐款5元的占总人数的分数即可得到捐款5元的人数是多少,列式解答即可得到答案;
(3)可用捐款总人数乘捐款20元占捐款总人数的分数就是捐款20元的人数,用捐款的总人数乘15%就是捐款50元的人数,用捐款的总人数乘$\frac{1}{8}$就可得到捐款100元的人数,然后再用得到的人数乘相应的钱数,相加后再除以捐款的人数就是全班平均每人捐款的钱数,列式解答即可得到答案.
解答 解:(1)$\frac{90}{360}=\frac{1}{4}$,
$10÷\frac{1}{4}=40$(人);
答:六(2)班共有40名学生;
(2)40×(1-$\frac{90}{360}$-$\frac{135}{360}$-15%-$\frac{1}{8}$)
=40×(1-$\frac{9}{10}$),
=40×$\frac{1}{10}$,
=4(人);
答:捐款5元的人数是4人;
(3)捐5元的人数为4人;
捐10元的人数为10人;
捐20元的人数为:$40×\frac{135}{360}=15$(人);
捐50元的人数为:$40×\frac{15}{100}=6$(人);
捐100元的人数为:$40×\frac{1}{8}=5$(人);
捐款总额为:5×4+10×10+20×15+50×6+100×5=1220(元).
平均每人捐款为:1220÷40=30.5(元)
答:全班平均每人捐款30.5元.
点评 本题主要考查条形统计图和扇形统计图,解答此题的关键是找准单位“1”,根据捐款10元的人数有10人确定全班捐款的总人数,然后再列式解答即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 11 | 14 | 12 | 15 | x | 13 | 12 | 10 |
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
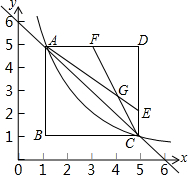 如图,若直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,其中∠B=∠D=90°,F为AD的中点,点E在边CD上,且DE=3EC,AE与CF相交于点G.
如图,若直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,其中∠B=∠D=90°,F为AD的中点,点E在边CD上,且DE=3EC,AE与CF相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 冷水加热过程中小气泡上升成为大气泡 | |
| B. | 投篮时的篮球运动 | |
| C. | 急刹车时汽车在地面上的滑动 | |
| D. | 随风飘动的树叶在空中的运动 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
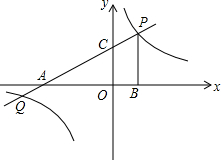 如图,直线y=$\frac{1}{2}$x+b,分别交x轴,y轴于点A、C,点P是直线AC与双曲线y=$\frac{k}{x}$在第一象限内的交点,过点P作PB⊥x轴于点B,若OB=2,PB=3
如图,直线y=$\frac{1}{2}$x+b,分别交x轴,y轴于点A、C,点P是直线AC与双曲线y=$\frac{k}{x}$在第一象限内的交点,过点P作PB⊥x轴于点B,若OB=2,PB=3查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com