Question

3．如图，在△ABC中，AD平分∠BAC，且$\frac{AD}{BD}$=$\frac{DC}{AD}$；若∠ADB=45°，求∠ACB的度数．

Answer 1

分析 如图，延长AD到E使得AD=DE，首先证明△ADB∽△CDE，得到∠BAD=∠DCE，推出A、B、E、C四点共圆，设圆心为O，连接EO交BC于F，连接OA，OC，EC，再证明△OEC是等边三角形，即可解决问题．

解答 解：如图，延长AD到E使得AD=DE．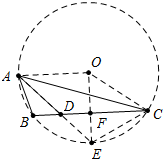

∵AD²=BD•DC，
∴$\frac{AD}{DC}$=$\frac{BD}{AD}$，∵∠ADB=∠CDE，
∴△ADB∽△CDE，
∴∠BAD=∠DCE，
∴A、B、E、C四点共圆，设圆心为O，连接EO交BC于F，连接OA，OC，EC．
∵AD平分∠BAC，
∴∠EAB=∠EAC，
∴$\widehat{BE}$=$\widehat{EC}$，
∴OE⊥CB，
∵∠ADB=∠EDF=45°，
∴∠DEF=45°，
∵OA=OE，
∴∠OAE=∠OEA=45°，
∴∠AOE=90°，
∴∠AOE=∠DFE，
∴OA∥DF，
∵AD=DE，
∴OF=EF，
∴CO=CE，∵OC=OE，
∴OC=OE=EC，
∴△OCE是等边三角形，
∴∠OCF=$\frac{1}{2}$∠OCE=30°，
∵OA=OC，OA∥BC，
∴∠OAC=∠OCA=∠ACB，
∴ACB=$\frac{1}{2}$∠OCD=$\frac{1}{2}$×30°=15°．

点评 本题考查相似三角形的判定和性质、等边三角形的判定和性质、四点共圆等知识，解题的关键是学会添加辅助线，构造相似三角形解决问题，题目比较难，辅助线比较多，属于中考压轴题．