
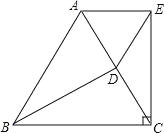
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.
【答案】(1)证明详见解析;(2) 等边三角形,理由详见解析.
【解析】
试题分析:(1)易证∠ACE=∠CBD,BC=AC,即可证明△BDA≌△CEA,即可解题;
(2)根据(1)中结论可得AE=CD,根据直角三角形中30°角所对直角边是斜边一半的性质可得DE=AD,即可解题.
试题解析:(1)∵D是AC中点,
∴∠CBD=∠ABD=30°,∠BDA=90°,
∵∠ACB=60°,
∴∠ACE=30°,
在△BDA和△CEA中,
∠BDA=∠CEA,∠ACE=∠ABD,AB=AC,
∴△BDA≌△CEA(AAS);
(2)等边三角形,理由如下:
∵△BDA≌△CEA,
∴AE=CD,
∵Rt△AEC中,∠ACE=30°,
∴DE=![]() AC=AD,
AC=AD,
∵AD=CD,
∴AD=DE=AE,
所以△ADE是等边三角形.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,1)、D(-![]() ,0),作直线AD并以线段AD为一边向上作正方形ABCD.
,0),作直线AD并以线段AD为一边向上作正方形ABCD.
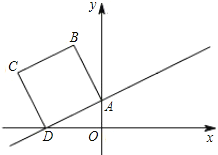
(1)填空:点B的坐标为________,点C的坐标为_________.
(2)若正方形以每秒2个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
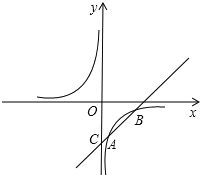
【题目】如图,已知反比例函数y =![]() 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
A.20°或100°
B.120°
C.20°或120°
D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推行公立医院改革,某医院将某药品经过两次降价,每瓶零售价由168元降为128元.已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得( )
A. 168(1+x)2=128 B. 168(1-x)2=128 C. 168(1-2x)=128 D. 168(1-x2)=128
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名运动员参加4×100米接力赛,甲必须为第一接力棒或第四接力棒的运动员,那么这四名运动员在比赛过程的接棒顺序有( )
A. 3种 B. 4种 C. 6种 D. 12种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com