
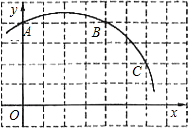
 如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).
如图,直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2).分析 (1)由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点P;
(2)由作图容易得出点P的坐标;连接PA、PC,作CD⊥x轴于D,由SAS证明△AOP≌△PDC,得出对应角相等∠OAP=∠DPC,再由角的互余关系,即可得出∠APC=90°;
(3)弓形ABC的面积=扇形PABC的面积-△APC的面积,即可得出结果;
(4)设圆锥的底面半径为r,由$\widehat{ABC}$的长=$\frac{90π•2\sqrt{5}}{180}$=2πr,即可求出r.
解答 解:(1)如图1所示: P就是求作的点;
P就是求作的点;
(2)由作图得:点P在x轴上,点P坐标为:(2,0);
连接PA、PC,作CD⊥x轴于D,如图2所示:
则OA=4,OP=CD=2,OD=6,DP=6-2=4,∠CDP=∠POA=90°,
∴OA=DP,
在△AOP和△PDC中,$\left\{\begin{array}{l}{OA=DP}&{\;}\\{∠POA=∠CDP}&{\;}\\{OP=DC}&{\;}\end{array}\right.$,
∴△AOP≌△PDC(SAS),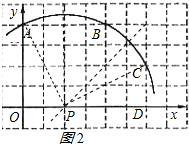
∴∠OAP=∠DPC,
∵∠OAP+∠OPA=90°,
∴∠DPC+∠OPA=90°,
∴∠APC=90°;
(3)如图3所示:
弓形ABC的面积=扇形PABC的面积-△APC的面积
=$\frac{90π•(2\sqrt{5})^{2}}{360}$-$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{5}$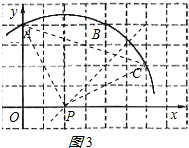
=5π-10;
(4)把扇形PAC围成一个圆锥,设圆锥的底面半径为r,
则$\widehat{ABC}$的长=$\frac{90π•2\sqrt{5}}{180}$=2πr,
∴r=$\frac{\sqrt{5}}{2}$,
即围成圆锥的底面半径为$\frac{{\sqrt{5}}}{2}$.
点评 本题是圆的综合题目,考查了确定圆心的方法、线段垂直平分线、全等三角形的判定与性质、弧长公式、扇形面积公式、圆的周长等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:解答题
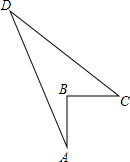 如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com