
 抛物线y=x2-mx-3与x轴交于点A、B,与y轴交于点C,其中点A的坐标为(1+m,0).
抛物线y=x2-mx-3与x轴交于点A、B,与y轴交于点C,其中点A的坐标为(1+m,0).分析 (1)用待定系数法求出抛物线解析式,再配成顶点式,即可确定出顶点坐标;
(2)先利用对称性得出点E,F坐标,再根据(1)得出的,画出抛物线的图象,和图象G的变化情况图,最后借助图象得出k的范围,注意用直线和抛物线只有一个交点时的k值.
解答 解:(1)∵ 抛物线y=x2-mx-3与x轴交于点A(1+m,0)、B,
抛物线y=x2-mx-3与x轴交于点A(1+m,0)、B,
∴(m+1)2-m(m+1)-3=0,
∴m=-1,
∴抛物线的解析式为y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为D(1,-4),
(2)如图,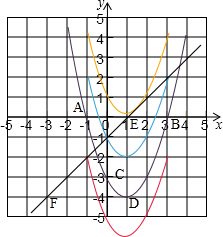
∵点A(-1,0)关于y轴的对称点为点E,
∴E(1,0),
∵点D关于直线y=-1的对称点为点F,
∴F(-3,4),
由图象有,-2≤k<2或$\frac{17}{4}$.
点评 本题是抛物线与x轴的交点题目,主要考查了二次函数图象与几何变换,待定系数法求一次函数、二次函数解析式.在求有关于平移的题目时,一定要数形结合,这样可以使抽象的问题变得具体化,降低了解题的难度与梯度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
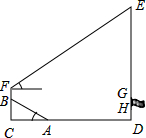 某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).
某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com