
��ƽ��ֱ������ϵx Oy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����
Oy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����
��1����b��c��ֵ����д���������ߵĶԳ���Ͷ������ꣻ
��2���������ߵĶԳ���Ϊֱ��l����P��m��n�������������ڵ�һ���ĵ㣬��E���P����ֱ��l�Գƣ���E���F����y��Գƣ����ı���OAPF�����Ϊ48�����P�����ꣻ
��3���ڣ�2���������£���M��ֱ��l������һ�㣬���ж�MP+MA�Ƿ������Сֵ�������ڣ���������Сֵ����Ӧ�ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
�⣺��1����������y=x2+bx+c����A��4��0����B��1����3����
�� ��
��
��ã�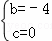 ��
��
��y=x2��4x=��x��2��2��4��
�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����ͼ1��
�ߵ�P��m��n�����E����ֱ��x=2�Գƣ�
���E��������4��m��n����
�ߵ�E���F����y��Գƣ�
���F��������m��4��n����
��PF=m����m��4��=4��
��PF=OA=4��
��PF��OA��
���ı���OAPF��ƽ���ı��Σ�
��S▱OAPF=OA• =4n=48��
=4n=48��
��n=12��
��m2��4m=n=12��
��ã�m1=6��m2=��2��
�ߵ�P�����������ڵ�һ���ĵ㣬
��m=6��
���P��������6��12����
��3������E��EH��x�ᣬ����ΪH����ͼ2��
�ڣ�2���������£���P��6��12����E����2��12����
��AH=4������2��=6��EH=12��
��EH��x�ᣬ����EHA=90�㣬
��EA2=EH2+AH2=122+62=180��
��EA=6 ��
��
�ߵ�E���P����ֱ��l�Գƣ�
��MP=ME��
��MP+MA=ME+MA��
���ݡ�����֮���߶���̡��ɵã�
����E��M��A����ʱ��MP+MA��С����Сֵ����EA�ij�����6 ��
��




 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
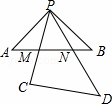
��ͼ�����㹻��ĵ���ֱ�����ǰ�PCD����Ƕ���P������һ������ֱ�����ǰ�PAB��ֱ�Ƕ��㴦�����ǰ�PCD�Ƶ�P��ƽ����ת�����ҡ�CPD������ʼ����б��AB�ཻ��PC��AB�ڵ�M��PD��AB�ڵ�N����AB=2��AN=x��BM=y�����ܷ�ӳy��x�ĺ�����ϵ��ͼ������ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
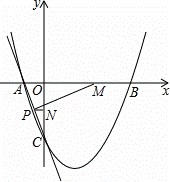
��ͼ��ֱ��y=��3x��3��x�ᡢy��ֱ��ཻ�ڵ�A��C��������C�ҶԳ���Ϊx=1��������y=ax2+bx+c��x���ཻ��A��B���㣮
��1�������A��C�����ꣻ
��2���������ߵĽ���ʽ��
��3������M���߶�AB����ÿ��1����λ���ȵ��ٶ��ɵ�B���A�˶���ͬʱ����N���߶�OC������ͬ���ٶ��ɵ�O���C�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�������PN��x�ᣬ��AC��P�������˶������У��߶�PM�ij����Ƿ������Сֵ�����У��������Сֵ�����ޣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������к�������y=2x��1����y=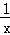 ����y=��x2��������ȡһ��������ȡ���ĺ���������������x��1ʱ������ֵy��x�������С���ĸ�������
����y=��x2��������ȡһ��������ȡ���ĺ���������������x��1ʱ������ֵy��x�������С���ĸ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ֱ��a��b������DC��ֱ��a�ཻ�ڵ�C������D��DE��b�ڵ�E����֪��1=25�㣬���2�Ķ���Ϊ��������

| �� | A�� | 115�� | B�� | 125�� | C�� | 155�� | D�� | 165�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���� ��ֵ��������
��ֵ��������
| �� | A�� | ��3��4֮�� | B�� | ��4��5֮�� | C�� | ��5��6֮�� | D�� | ��6��7֮�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com