
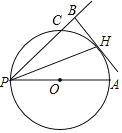
【题目】如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.
(1)求证:HB是⊙O的切线;
(2)若HB=4,BC=2,求⊙O的直径.
【答案】(1)详见解析;(2)10.
【解析】
(1)连接OH,由题意可得∠OHP=∠HPA=∠HPB,可证OH∥BP,则可得OH⊥BH,根据切线的判定可证HB是⊙O的切线;
(2)过点O作OE⊥PC,垂足为E,可证四边形EOHB是矩形,可得OE=BH=4,OH=BE,再根据勾股定理可求OP的长,即可得⊙O的直径.
证明:(1)如图,连接OH,
∵PH平分∠APB,
∴∠HPA=∠HPB,
∵OP=OH,
∴∠OHP=∠HPA,
∴∠HPB=∠OHP,
∴OH∥BP,
∵BP⊥BH,
∴OH⊥BH,
∴HB是⊙O的切线;
(2)如图,过点O作OE⊥PC,垂足为E,
∵OE⊥PC,OH⊥BH,BP⊥BH,
∴四边形EOHB是矩形,
∴OE=BH=4,OH=BE,
∴CE=OH﹣2,
∵OE⊥PC
∴PE=EC=OH﹣2=OP﹣2,
在Rt△POE中,OP2=PE2+OE2,
∴OP2=(OP﹣2)2+16
∴OP=5,
∴AP=2OP=10,
∴⊙O的直径是10.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
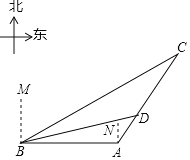
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
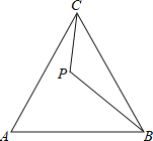
【题目】如图所示,点P位于等边△ABC的内部,且∠ACP=∠CBP.
(1)延长BP至点D,使得PD=PC,连接AD,CD.
①依题意,补全图形;
②证明:AD+CD=BD;
(2)在(1)的条件下,若BD的长为2,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列![]() (边长为1)的网格中,已知
(边长为1)的网格中,已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 在格点上,请分别按不同要求在网格中描出一个格点
在格点上,请分别按不同要求在网格中描出一个格点![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(1)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后所得的三角形,点
,画出旋转后所得的三角形,点![]() 旋转后落点为
旋转后落点为![]() .
.
(2)经过![]() ,
,![]() ,
,![]() 三点有一条抛物线,请找到点
三点有一条抛物线,请找到点![]() ,使点
,使点![]() 也落在这条抛物线上.
也落在这条抛物线上.
(3)经过![]() ,
,![]() ,
,![]() 三点有一个圆,请找到一个横坐标为2的点
三点有一个圆,请找到一个横坐标为2的点![]() ,使点
,使点![]() 也落在这个圆上.
也落在这个圆上.
(1)点![]() 的坐标为( , )
的坐标为( , )
(2)点![]() 的坐标为( , )/span>
的坐标为( , )/span>
(3)点![]() 的坐标为( , )
的坐标为( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
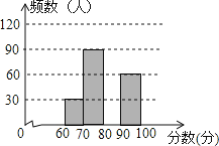
【题目】 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |
(1)此次调查的样本容量为______;m=______;n=______;
(2)补全频数分布直方图;
(3)如果比赛成绩80分以上为优秀,那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是______名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A(-1,0),点B,与y轴交于点C(0,-3),作直线BC.点P是抛物线的对称轴上的一个动点,P点到x轴和直线BC的距离分别为PD、PE.
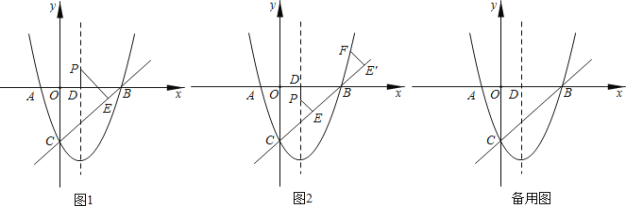
(1)求抛物线解析式;
(2)当P点运动过程中满足PE=PD时,求此时点P的坐标;
(3)如图2,从点B处沿着直线BC的垂线翻折PE得到FE',当点F在抛物线上时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?
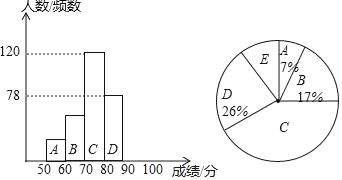
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com