
【题目】对于任意一个自然数![]() ,如果
,如果![]() 的各个数位上的数字之和是一个整数的平方,那么称
的各个数位上的数字之和是一个整数的平方,那么称![]() 为“方数”,例如,自然数32587各位数字之和是
为“方数”,例如,自然数32587各位数字之和是![]() ,所以32587就是一个“方数”;对于任意一个自然数
,所以32587就是一个“方数”;对于任意一个自然数![]() ,如果
,如果![]() 是一个整数的立方,那么称
是一个整数的立方,那么称![]() 为“立方数”,例如,
为“立方数”,例如,![]() ,所以8是一个立方数.
,所以8是一个立方数.
(1)判断9999是不是方数?729是不是立方数?
(2)若一个两位数各位数字之和是一个“立方数”,并且各位数字相差4,请求出这个两位数;
(3)若自然数![]() 既是“方数”又是“立方数”,则称
既是“方数”又是“立方数”,则称![]() 为完美数,请直接写出小于1000的自然数中的所有完美数.
为完美数,请直接写出小于1000的自然数中的所有完美数.
【答案】(1)9999是方数,729是立方数;(2)62或26.(3)27,216.
【解析】
(1)根据“方数”和“立方数”的定义直接判断即可;
(2)首先判断出两位数数位上的数字之和的范围,在此范围内判断出立方数,由此可计算出数位上各数字即可解决问题;
(3)首先判断出1000之内的立方数,再判断出这些立方数中的方数即可解决问题.
(1)∵9+9+9+9=36=62,
∴9999是一个“方数”;
∵729=93,
∴729是一个“立方数”.
(2)可设x,y是一个两位数十位上的数字和个位上的数字(x,y均为整数),则:1≤x≤9,1≤y≤9,
∴2≤x+y≤18,
∵2与18之间的立方数只有8,
∴x+y=8,
∵x-y=4或y-x=4,
∴![]() 或
或![]()
解得![]() 或
或![]() ,
,
所以,这个两位数是62或26.
(2)小于1000的立方数有:8,27,64,125,216,343,512,729,
∴27各数位上数字和=2+7=9=32,
∴27是“方数”;
216各数位上数字和=2+1+6=9=32,
∴216是“方数”;
∴小于1000的“完美数”是27,216.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤![]() 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;
⑥![]() 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;
⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分![]() ,BN
,BN![]() AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
AN于点N,延长BN交AC于点D,已知AB=10,AC=16.

(1)求证:BN=DN;
(2)求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列按照一定规律排列一组图形,其中图形①中共有2个小三角形,图形②中共有6个小“三角形,图形③中共有11个小三角形,图形④中共有17个小三角形,……,按此规律,图形⑧中共有![]() 个小三角形,这里的
个小三角形,这里的![]() ( ).
( ).

A.32B.41C.51D.53
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代一部数学专著,其中第八卷《方程》记载:“今有五雀六燕,集称之衝,雀俱重,燕俱轻,一雀一燕交而处,衡视平”,意思是“五只雀比六只燕重.但是将这群雀和这群燕互相交换一只以后,两群鸟一样重,如果假设一只雀重x两,则用含x的式子表示一只燕的重量为_____两.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是( )

A.110°B.100°C.90°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一个污水净化塔内部,污水从上方入口进入后,流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有
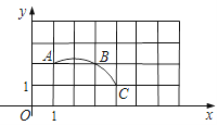
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com