
 PE?请写出探究结果,并说明理由.
PE?请写出探究结果,并说明理由.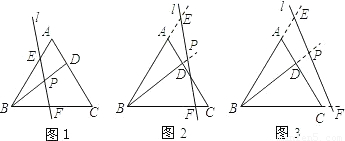
 PE能得出什么结论.根据△BPF∽△EBF,可得BF2=PF•EF=3PF2,因此BF=
PE能得出什么结论.根据△BPF∽△EBF,可得BF2=PF•EF=3PF2,因此BF=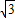 PF,且∠BPF=60°,∵∠PFB=90°,∴∠PBF=90-60=30°,因此当BD平分∠ABC时,PF=
PF,且∠BPF=60°,∵∠PFB=90°,∴∠PBF=90-60=30°,因此当BD平分∠ABC时,PF= PE.
PE. PE.
PE. PB.
PB. PE.
PE.

科目:初中数学 来源:2008年全国中考数学试题汇编《概率》(02)(解析版) 题型:选择题




查看答案和解析>>
科目:初中数学 来源:2010年山东省泰安市初中学业考试数学样卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2008年山东省泰安市中考数学试卷(解析版) 题型:选择题




查看答案和解析>>
科目:初中数学 来源:2008年山东省泰安市中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com