练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

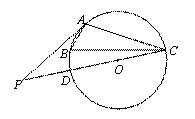
    如图，已知A、B、C分别是⊙O上的点，∠B=60°，P是直径CD的延长线上的一点，且AP=AC.

    （1）求证：AP与⊙O相切；

    （2）如果AC=3，求PD的长.


    （1）证明：连接OA.

    ∵.

    ∴.

    ∴.

    ∵OA=OC,

    ∴.

    ∵AP=AC,

    ∴.

    ∴.

    ∴.

    又∵点A在⊙O上，

    ∴PA是⊙O的切线.    

     (2)在Rt△PAO中，，

    ∴.

    又∵AC=3，

    ∴AP=AC=3.

                   根据勾股定理得: .   

    ∴，.

    ∴.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    -2的绝对值是

      A．-2               B．2              C．             D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


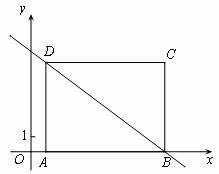
    如图，在平面直角坐标系xOy中，矩形ABCD的边AD=6，A（1，0）， B（9，0），直线y=kx+b经过B、D两点．

    （1）求直线y=kx+b的表达式；

    （2）将直线y=kx+b平移，当它l与矩形没有公共点时，直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    把多项式分解因式，结果为        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     已知，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    的相反数是

    A．3           B．           C．     D．   

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一列不全为零的数除了第一个数和最后一个数外，每个数都等于前后与它相邻的两数之和，则称这列数具有“波动性质”.已知一列数共有18个，且具有“波动性质”，则这18个数的和为     

    A．-64            B．0           C．18                D．64

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“匀称三角形”

    （1）已知：如图1，在△ABC中，∠C=90°，,.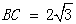

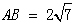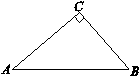
    求证：△ABC是“匀称三角形”；

                                                                     图1

    （2）在平面直角坐标系xoy中，如果三角形的一边在x轴上，且这边的中线恰好等于这边的长，我们又称这个三角形为“水平匀称三角形”.如图2，现有10个边长是1的小正方形组成的长方形区域记为G, 每个小正方形的顶点称为格点，A（3，0），B（4，0），若C、D（C、D两点与O不重合）是x轴上的格点，且点C在点A的左侧. 在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个？其中是否存在横坐标为整数的点P，如果存在请求出这个点P的坐标，如果不存在请说明理由.

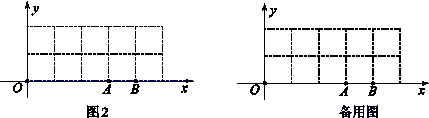
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（    ）

    A.100°       B.80°           C.70°            D.50°

       

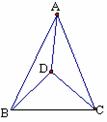
    查看答案和解析>>

    同步练习册答案