
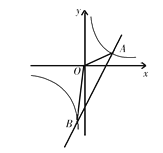
【题目】如图,直线y1=3x﹣5与反比例函数y2=![]() 的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
(1)求k和n的值;
(2)求△AOB的面积;
(3)直接写出y1> y2时自变量x的取值范围.
【答案】(1)k=3,n=;(2)![]() ;(3)
;(3)![]() 或 x>2.
或 x>2.
【解析】
(1)把A,B的坐标代入直线的解析式求出m,n的值,再把B点坐标代入反比例函数解析式求出k的值;
(2)先求出直线与x轴、y轴的交点坐标,再求出即可.
(3)由图象可知取一次函数图象在反比例函数图象上方的x的取值范围即可.
解:(1)∵点B(n,﹣6)在直线y=3x﹣5上.
∴-6=3n-5,解得:n=![]() .
.
∴B(![]() ,-6);
,-6);
∵反比例函数![]() 的图象也经过点B(
的图象也经过点B(![]() ,-6),
,-6),
∴k-1=-6×(![]() )=2,解得:k=3;
)=2,解得:k=3;
(2)设直线y=3x﹣5分别与x轴,y轴相交于点C,点D,
当y=0时,即3x﹣5=0,x=![]() ,
,
∴OC=![]() ,
,
当x=0时,y=3×0-5=-5,
∴OD=5,
∵点A(2,m)在直线y=3x﹣5上,
∴m=3×2-5=1,即A(2,1).
![]() .
.
(3)由图象可知y1> y2时自变量x的取值范围为:![]() 或 x>2.
或 x>2.



科目:初中数学 来源: 题型:
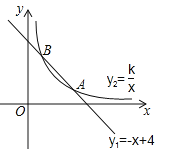
【题目】如图,函数![]() 的图象与函数
的图象与函数![]() (x>0)的图象交于A(m,1),B(1,n)两点.
(x>0)的图象交于A(m,1),B(1,n)两点.
(1)求k,m,n的值;
(2)利用图象写出当x≥1时,![]() 和
和![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
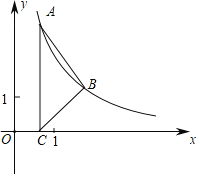
【题目】如图,在平面直角坐标系中,双曲线l:y=![]() (x>0)过点A(a,b),B(2,1)(0<a<2);过点A作AC⊥x轴,垂足为C.
(x>0)过点A(a,b),B(2,1)(0<a<2);过点A作AC⊥x轴,垂足为C.
(1)求l的解析式;
(2)当△ABC的面积为2时,求点A的坐标;
(3)点P为l上一段曲线AB(包括A,B两点)的动点,直线l1:y=mx+1过点P;在(2)的条件下,若y=mx+1具有y随x增大而增大的特点,请直接写出m的取值范围.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面内有一个△ABC,O为平面内的一点,延长AO到A′,使OA′=OA,延长BO到B′,使OB′=OB,延长CO到从C′,使OC′=OC,得到△A′B′C′,问:△A′B′C′与△ABC是否全等?这两个三角形的对应边是否平行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料1:在处理分数和分式问题时,有时由于分子比分母大,或者分子的次数高于分母的次数,在实际运算时往往难度比较大,这时我们可以将假分数(分式)拆分成一个整数(整式)与一个真分数(式)的和(差)的形式,通过对简单式的分析来解决问题,我们称之为分离整数法.此法在处理分式或整除问题时颇为有效.
例:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:设x+2=t,则x=t﹣2.
∴原式=![]()
∴![]()
这样,分式![]() 就拆分成一个整式(x﹣5)与一个分式
就拆分成一个整式(x﹣5)与一个分式![]() 的和的形式.
的和的形式.
根据以上阅读材料回答下列问题:
(1)将分式![]() 拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 ;
拆分成一个整式与一个分子为整数的分式的和的形式,则结果为 ;
(2)已知分式![]() 的值为整数,求整数x的值;
的值为整数,求整数x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
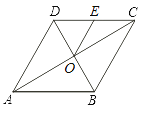
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).
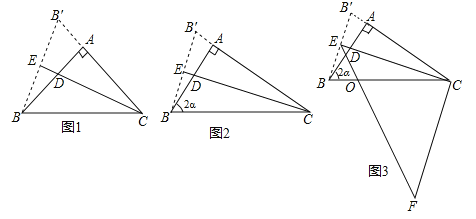
(1)如图1,若AB=AC,求证:CD=2BE;
(2)如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);
(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1,△COF的面积为S2,求![]() (用含α的式子表示).
(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
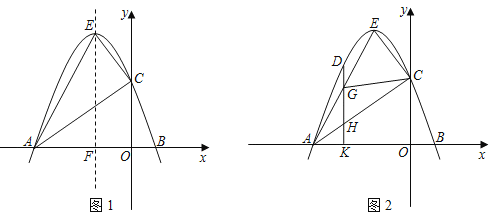
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com