
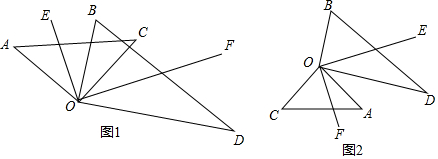
分析 (1)根据余角的性质即可得到结论;
(2)根据角平分线的定义得到∠BOE=$\frac{1}{2}∠$AOB,∠DOF=$\frac{1}{2}∠$COD,得到∠BOE=∠DOF,等量代换得到结论;
(3)根据角平分线的性质得到∠AOE=$\frac{1}{2}∠$AOB,∠COF=$\frac{1}{2}∠$COD,求得∠AOE=∠COF,等量代换得到结论.
解答 解:(1)相等,
理由:∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD;
故答案为:相等;
(2)∵OE平分∠AOB,OF平分∠COD,
∴∠BOE=$\frac{1}{2}∠$AOB,∠DOF=$\frac{1}{2}∠$COD,
∵∠AOB=∠COD,
∴∠BOE=∠DOF,
∵∠EOF=∠BOE+∠BOC+∠COF=∠DOF+∠COF+∠BOC=90°;
(3)不变,
理由:∵OE平分∠AOB,OF平分∠COD,
∴∠AOE=$\frac{1}{2}∠$AOB,∠COF=$\frac{1}{2}∠$COD,
∵∠AOB=∠COD,
∴∠AOE=∠COF,
∵∠EOF=∠AOE+∠AOF=∠COF+∠AOF=90°.
点评 本题考查了余角的性质,角平分线的定义,正确的识别图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (2-x)(2+x)=4-x2 | B. | -a(a-b)=-a2+ab | C. | m2-n2=(m+n)(m-n) | D. | (1-x)2=(x-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(2x-1)=2x2-1 | B. | x2-9=(x-3)( x+3 ) | C. | (a+2)2=a2+4 | D. | (x+2)(x-3)=x2+x-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50×109千克 | B. | 5×1010千克 | C. | 5×1011千克 | D. | 0.5×1012千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆的周长与它的半径之比是一个不变的常数 | |
| B. | 圆的面积与它的半径之比是一个不变的常数 | |
| C. | 圆周率是一个确定的值,它的准确值是π,它是一个无限不循环小数 | |
| D. | 圆周率是一个确定的值,它的一个近似值是3.14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
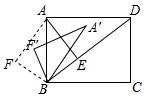 如图,矩形ABCD中,AB=2,AD=2$\sqrt{3}$,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF,将△ABF绕点B顺时针旋转一个α(90°<α<180°)记旋转中的△ABF为△A′B′F′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ是等腰三角形,且DP=DQ,则DQ的长为4-$\sqrt{6}$+$\sqrt{2}$.
如图,矩形ABCD中,AB=2,AD=2$\sqrt{3}$,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF,将△ABF绕点B顺时针旋转一个α(90°<α<180°)记旋转中的△ABF为△A′B′F′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ是等腰三角形,且DP=DQ,则DQ的长为4-$\sqrt{6}$+$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com