
【题目】如图,已知正比例函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
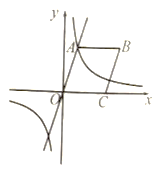
(1)填空:![]() 的值为_______________,
的值为_______________,![]() 的值为_____________;
的值为_____________;
(2)以点![]() 为圆心、
为圆心、![]() 为半径画弧交
为半径画弧交![]() 轴的正半轴于点
轴的正半轴于点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)观察上述反比例函数![]() 的图象,当
的图象,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据点![]() (1,
(1,![]() )在正比例函数
)在正比例函数![]() 与反比例函数
与反比例函数![]() 的图象上,将点A代入函数解析式求解即可;
的图象上,将点A代入函数解析式求解即可;
(2)根据题干作图方法和平行线性质,判断四边形OABC是菱形,再利用勾股定理进行计算即可求解;
(3)根据反比例函数图像性质求解即可.
解:(1)∵点A(1,a)为![]() 与
与![]() 的交点,
的交点,
∴将点A(1,a)代入![]() ,得
,得![]() ,
,
∴点A(1,3),
再将点A(1,3)代入![]() ,得
,得![]() ,
,
故答案为:![]() ,
,![]() ;
;
(2)如图,延长BA交y轴于点E,
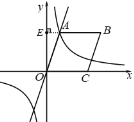
∵AB∥OC,
∴BE⊥y轴,
∴OE=3,AE=1,
由题意可知,OA=OC,
∴四边形OABC是菱形,
∴AB=OA=![]() ,
,
∴BE=![]() ,
,
∴点B的坐标为(![]() ,3);
,3);
(3)当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∵在第三象限图像中,y随x的增大而减小,
∴当![]() 时,
时,![]() ,
,
∵在第一象限的图像中,![]() 时,
时,![]() ,
,
综上:当![]() 时,x的取值范围为:
时,x的取值范围为:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
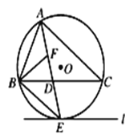
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,![]() 的三个顶点的分别为
的三个顶点的分别为![]() ,
,![]() ,
,![]() (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).

(1)在网格内画出![]() 向下平移2个单位长度得到的
向下平移2个单位长度得到的![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(2)以点![]() 为位似中心,在网格内画出
为位似中心,在网格内画出![]() ,使
,使![]() 与
与![]() 位似,且位似比为
位似,且位似比为![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(3)![]() 的面积是________平方单位.
的面积是________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 地和
地和![]() 地之间有一条笔直的公路,一天,甲车从
地之间有一条笔直的公路,一天,甲车从![]() 地去
地去![]() 地,乙车从
地,乙车从![]() 地去
地去![]() 地,乙先出发,若甲、乙之间的距离为
地,乙先出发,若甲、乙之间的距离为![]() 千米,行驶时间为
千米,行驶时间为![]() 小时,
小时,![]() 与
与![]() 之间的函数关系如图所示,则下列说法错误的是 ( )
之间的函数关系如图所示,则下列说法错误的是 ( )

A.![]() 两地间距离为100千米B.甲车的速度是80千米/时
两地间距离为100千米B.甲车的速度是80千米/时
C.甲到![]() 地比乙车到
地比乙车到![]() 地早
地早![]() 小时D.甲出发0.5小时后与乙车相遇
小时D.甲出发0.5小时后与乙车相遇
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行职工五人制足球联赛,共赛 17 轮(即每队均需参赛 17 场),记分办法是胜一场得 3分,平一场得 1 分,负一场得 0 分 . 若![]() 足球队总积分为 16 分,且踢平场数是所负场数的整数倍,试推算
足球队总积分为 16 分,且踢平场数是所负场数的整数倍,试推算![]() 足球队所负场数的情况有( )
足球队所负场数的情况有( )
A.1 种B.2 种C.3 种D.4 种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来佳木斯市旅游事业发展迅速,“大亮子河森林公园”“富锦国家湿地公园”“赫哲民族文化村”“大来岗达勒花海”等景区愈来愈为人们所知晓 . 在一次调查中,根据市民对这四个景区的了解情况,按答题分数分为![]() . 比较熟悉;
. 比较熟悉; ![]() . 基本了解;
. 基本了解; ![]() . 略有知晓;
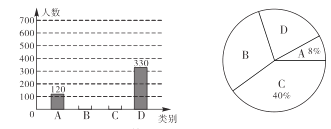
. 略有知晓; ![]() . 知之甚少,四类进行统计,绘制了以下两幅统计图(不完整),请根据图中信息解答以下各题:
. 知之甚少,四类进行统计,绘制了以下两幅统计图(不完整),请根据图中信息解答以下各题:
(1)本次调查活动的样本容量是 ;
(2)补全条形统计图;
(3)“略有知晓”类占扇形统计图的圆心角是多少度? “知之甚少”类市民占被调查人数的百分比是多少?
(4)已知某小区有 5000 人,那么估计对这些景区“比较熟悉”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
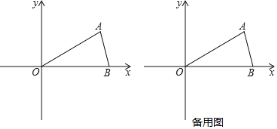
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】转转盘和摸球是等可能概率下的经典模型.
(1)在一个不透明的口袋中,放入除颜色外其余都相同的4个小球,其中1个白球,3个黑球搅匀后,随机同时摸出2个球,求摸出两个都是黑球的概率(要求釆用树状图或列表法求解);
(2)如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com