
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

【答案】(1) y=﹣![]() ;(2) x<﹣4 或 0<x<4;(3) y=-
;(2) x<﹣4 或 0<x<4;(3) y=-![]() .
.
【解析】
(1)直线l1:y= -![]() x经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;(2)根据图象得到点B的坐标,进而直接得到﹣
x经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;(2)根据图象得到点B的坐标,进而直接得到﹣ ![]() x>
x> ![]() 的解集即可;(3)设平移后的直线
的解集即可;(3)设平移后的直线 ![]() 与 x 轴交于点 D,连接 AD,BD,由平行线的性质可得出S△ABC=S△ABF,即可得出关于OD的一元一次方程,解方程即可得出结论.
与 x 轴交于点 D,连接 AD,BD,由平行线的性质可得出S△ABC=S△ABF,即可得出关于OD的一元一次方程,解方程即可得出结论.
(1)∵直线 l1:y=﹣![]() x 经过点 A,A 点的纵坐标是 2,
x 经过点 A,A 点的纵坐标是 2,
∴当 y=2 时,x=﹣4,
∴A(﹣4,2),
∵反比例函数 y=![]() 的图象经过点 A,
的图象经过点 A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为 y=﹣![]() ;
;
(2)∵直线 l1:y=﹣![]() x 与反比例函数 y=
x 与反比例函数 y=![]() 的图象交于 A,B 两点,
的图象交于 A,B 两点,
∴B(4,﹣2),
∴不等式﹣ ![]() x>
x> ![]() 的解集为 x<﹣4 或 0<x<4;
的解集为 x<﹣4 或 0<x<4;
(3)如图,设平移后的直线 ![]() 与 x 轴交于点 D,连接 AD,BD,
与 x 轴交于点 D,连接 AD,BD,
∵CD∥AB,
∴△ABC 的面积与△ABD 的面积相等,
∵△ABC 的面积为 30,
∴S△AOD+S△BOD=30,即 ![]() OD(|yA|+|yB|)=30,
OD(|yA|+|yB|)=30,
∴![]() ×OD×4=30,
×OD×4=30,
∴OD=15,
∴D(15,0),
设平移后的直线 ![]() 的函数表达式为 y=﹣
的函数表达式为 y=﹣![]() x+b, 把 D(15,0)代入,可得 0=﹣
x+b, 把 D(15,0)代入,可得 0=﹣![]() ×15+b,
×15+b,
解得 b=![]() ,
,
∴平移后的直线![]() 的函数表达式为 y=-
的函数表达式为 y=-![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
(1)在点C(0,2),D(2,![]() ),E(4,1)中,线段AB的“临近点”是__________;
),E(4,1)中,线段AB的“临近点”是__________;
(2)若点M(m,n)在直线![]() 上,且是线段AB的“临近点”,求m的取值范围;
上,且是线段AB的“临近点”,求m的取值范围;
(3)若直线![]() 上存在线段AB的“临近点”,求b的取值范围.
上存在线段AB的“临近点”,求b的取值范围.
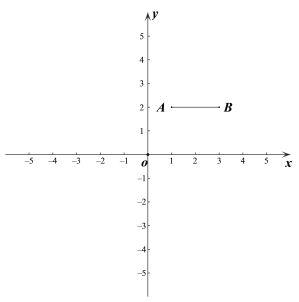
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
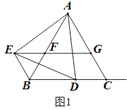
(1) 如图1,当点D在线段BC上时:
①求证:△AEB≌△ADC;②求证:四边形BCGE是平行四边形;
(2)如图2,当点D在BC的延长线上,且CD=BC时,试判断四边形BCGE是什么特殊的四边形?并说明理由.
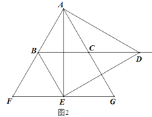
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象如下所示,下列5个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() (
(![]() 的实数),其中正确的结论有几个?
的实数),其中正确的结论有几个?
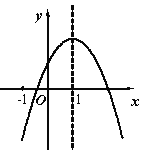
A. ①②③ B. ②③④ C. ②③⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
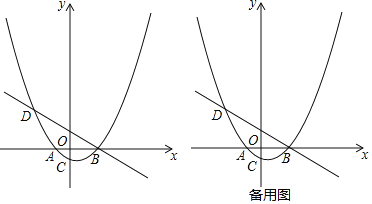
【题目】如图,已知抛物线y=a(x+2)(x-4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=-![]() x+b与抛物线的另一交点为D,且点D的横坐标为-5.
x+b与抛物线的另一交点为D,且点D的横坐标为-5.
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
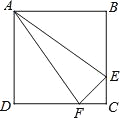
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. 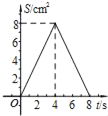 B.
B. 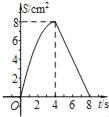
C. 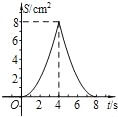 D.
D. 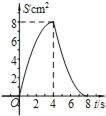
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
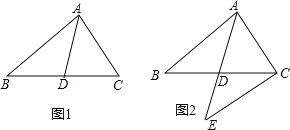
【题目】在△ABC中,D是边BC的中点.
(1)①如图1,求证:△ABD和△ACD的面积相等;
②如图2,延长AD至E,使DE=AD,连结CE,求证:AB=EC.
(2)当∠BAC=90°时,可以结合利用以上各题的结论,解决下列问题:
①求证:AD![]() BC(即:直角三角形斜边上的中线等于斜边的一半);
BC(即:直角三角形斜边上的中线等于斜边的一半);
②已知BC=4,将△ABD沿AD所在直线翻折,得到△ADB',若△ADB'与△ABC重合部分的面积等于△ABC面积的![]() ,请画出图形(草图)并求出AC的长度.
,请画出图形(草图)并求出AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形 OABC 是矩形,点 B 的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线 m 从原点O出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 m 与矩形 OABC 的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若 MN=![]() AC,求 t 的值;
AC,求 t 的值;
②设△OMN 的面积为S,当 t 为何值时,S=![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com