Question

1．已知抛物线y=ax²+bx+c与y轴交于A（0，-4），与x轴交于B、C两点，且B（-2，0）、C（4，0）．
（1）求抛物线的解析式；
（2）如图1，若点M在y轴上，且∠BMO+∠OAB=∠ACB，求点M的坐标；
（3）如图2，将抛物线y=ax²+bx+c向右平移n（n＞0）个单位得到的新抛物线与x轴交于M、N（M在N左侧），P为x轴下方的新抛物线上任意一点，连PM、PN，过P作PQ⊥MN于Q，$\frac{PQ}{MQ}$+$\frac{PQ}{NQ}$是否为定值？请说明理由．

Answer 1

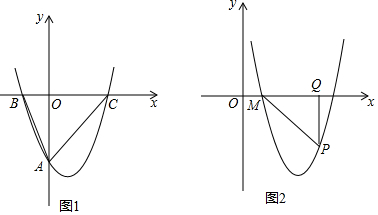
分析 （1）由题意设抛物线解析式为y=a（x+2）（x-4），把（0，-4）代入求出a即可．
（2）如图1中，在y轴上取点D（0，-2），M（0，-6）．连接BD、BM．由△BDA∽△MDB，推出∠BAO+∠BMO=45°，即点M满足条件，根据对称性求出点M′即可．
（3）如图2中，结论：$\frac{PQ}{MQ}$+$\frac{PQ}{NQ}$是定值，定值为3．抛物线y=ax²+bx+c向右平移n（n＞0）个单位得到的新抛物线与x轴交于M、N，在平移过程中，MN=6是定值，不妨把抛物线向左平移，使得顶点在y轴上，如图3中抛物线的解析式为y=$\frac{1}{2}$x²-$\frac{9}{2}$，OM=ON=3，设P（m，$\frac{1}{2}$m²-$\frac{9}{2}$），则MQ=3+m，NQ=3-m，代入式子化简即可解决问题．

解答 解：（1）由题意设抛物线解析式为y=a（x+2）（x-4），把（0，-4）代入得到a=$\frac{1}{2}$，
∴抛物线的解析式为y=$\frac{1}{2}$（x+2）（x-4）=$\frac{1}{2}$x²-x-4．

（2）如图1中，在y轴上取点D（0，-2），M（0，-6）．连接BD、BM．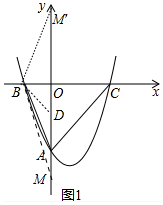

∵B（-2，0），A（0，-4），
∴BD=2$\sqrt{2}$，DA=2，DM=4，
∴$\frac{BD}{DM}$=$\frac{2\sqrt{2}}{4}$=$\frac{\sqrt{2}}{2}$，$\frac{DA}{BD}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$，
∴$\frac{BD}{DM}$=$\frac{DA}{BD}$，∵∠BDA=∠MDB，
∴△BDA∽△MDB，
∴∠DBA=∠BMD，
∵OB=OD，∠BOD=90°，
∴∠BDO=45°，
∵∠BDO=∠DBA+∠BAD，
∴∠BAO+∠BMO=45°，
∵∠BMO+∠OAB=∠ACB=45°，
∴点M满足条件，
根据对称性，点M关于x轴的对称点M′，也满足条件，
∴满足条件的点M的坐标为（0，-6）或（0，6）．

（3）如图2中，结论：$\frac{PQ}{MQ}$+$\frac{PQ}{NQ}$是定值，定值为3．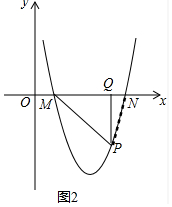

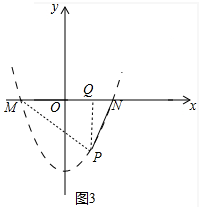
理由：抛物线y=ax²+bx+c向右平移n（n＞0）个单位得到的新抛物线与x轴交于M、N，
在平移过程中，MN=6是定值，不妨把抛物线向左平移，使得顶点在y轴上．如图3中，
∵图3中的抛物线的解析式为y=$\frac{1}{2}$x²-$\frac{9}{2}$，OM=ON=3，设P（m，$\frac{1}{2}$m²-$\frac{9}{2}$），则MQ=3+m，NQ=3-m，
∴$\frac{PQ}{MQ}$+$\frac{PQ}{NQ}$=PQ•（$\frac{1}{MQ}$+$\frac{1}{NQ}$）=（$\frac{9}{2}$-$\frac{1}{2}$m²）•（$\frac{1}{m+3}$+$\frac{1}{3-m}$）=$\frac{1}{2}$（9-m²）•$\frac{6}{9-{m}^{2}}$=3．
∴$\frac{PQ}{MQ}$+$\frac{PQ}{NQ}$为定值．

点评 本题考查二次函数综合题、相似三角形的判定和性质、定值问题等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，第三个问题解题的关键是把图形特殊化，题目比较难，属于中考压轴题．