
����Ŀ��(2016����������25��)
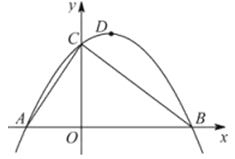
��ͼ����֪��A������Ϊ(-2��0)��ֱ��y=-![]() +3��x�ᣬy��ֱ��ڵ�B�͵�C,����AC������ΪD��������y=ax2+bx+c��A��B��C���㣮
+3��x�ᣬy��ֱ��ڵ�B�͵�C,����AC������ΪD��������y=ax2+bx+c��A��B��C���㣮
(1)��ֱ��д��B��C��������꣬�����ߵĽ���ʽ������D�����ꣻ
(2)�������ߵĶԳ���DE���߶�BC�ڵ�E��PΪ��һ��������������һ�㣬����P��x��Ĵ��ߣ����߶�BC�ڵ�F���ı���DEFPΪƽ���ı���,���P�����ꣻ
(3)����M���߶�BC�ϵ�һ���㣬����M��MN��AB����AC�ڵ�N��.Q�ӵ�B��������ÿ��l����λ���ȵ��ٶ����߶�BA���A�˶����˶�ʱ��Ϊt(��)����t(��)Ϊ��ֵʱ������QMNΪ����ֱ��������?
���𰸡���1��(1)B(4��O)��C(0��3)�������ߵĽ���ʽΪ![]() ����D������Ϊ
����D������Ϊ![]() ����2������P����Ϊ(3��
����2������P����Ϊ(3��![]() )ʱ���ı���DEFPΪƽ���ı��Σ���3����tΪ
)ʱ���ı���DEFPΪƽ���ı��Σ���3����tΪ![]() ��
��![]() ��
��![]() ʱ��������QMNΪ����ֱ�������Σ�
ʱ��������QMNΪ����ֱ�������Σ�
��������
�����������1����ֱ��y=-![]() +3�Ľ���ʽ���ɵ�B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ�����������ߵĽ���ʽ���ɵ������ߵĽ���ʽ����2�����P����Ϊ
+3�Ľ���ʽ���ɵ�B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ�����������ߵĽ���ʽ���ɵ������ߵĽ���ʽ����2�����P����Ϊ![]() ���F������Ϊ(m��-
���F������Ϊ(m��-![]() m+3)�������ı���DEFPΪƽ���ı��Σ���PF=DE���ɴ��з������m��ֵ�����ɵõ�P�����ꣻ��3���ֱ��Ե�M��N��QΪֱ�Ƕ������۽������.
m+3)�������ı���DEFPΪƽ���ı��Σ���PF=DE���ɴ��з������m��ֵ�����ɵõ�P�����ꣻ��3���ֱ��Ե�M��N��QΪֱ�Ƕ������۽������.
���������(1)B(4��O)��C(0��3)��
�����ߵĽ���ʽΪ![]()
����D������Ϊ![]()
(2)��x=1����![]()
���PΪ��һ��������������һ�㣬���Կ����P����Ϊ![]()
��F������Ϊ(m��-![]() m+3)�����ı���DEFPΪƽ���ı��Σ���PF=DE
m+3)�����ı���DEFPΪƽ���ı��Σ���PF=DE
��-![]() m2+
m2+![]() m+3-(-
m+3-(-![]() m+3)=
m+3)=![]()
��֮����m1=3,m2=1(�������⣬��ȥ)��
������P����Ϊ(3��![]() )ʱ���ı���DEFPΪƽ���ı��Σ�
)ʱ���ı���DEFPΪƽ���ı��Σ�
(3)���M������Ϊ(n��-![]() )��MN��y���ڵ�G��
)��MN��y���ڵ�G��
![]()
![]() ��BAC
��BAC![]()
������Q1MN=90����MN=MQ2=OGʱ��![]() ��֮��MN=2��
��֮��MN=2��
![]() ��֮��
��֮��![]()
����![]() ʱ���������
ʱ���������![]()
![]()
������MQ3N=90����Q3M=Q3Nʱ��![]() NM=Q3K=OG
NM=Q3K=OG
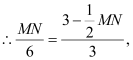 ��֮����MN=3��
��֮����MN=3��
![]()
![]() ��֮����n=2����
��֮����n=2����![]()
MN���е�K������Ϊ![]()
![]() ��
��![]()
����tΪ![]() ��
��![]() ��
��![]() ʱ��������QMNΪ����ֱ�������Σ�
ʱ��������QMNΪ����ֱ�������Σ�


 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2015��12��������

��1����ͼ����һ�����ο��ڱ��������ס4�����������Ͻǵ�һ����Ϊx�������������ú�x��ʽ�ӱ�ʾ��������С���������� �� �� ��
��2���ڱ��п�ס�ĸ���֮����С��Ϊa1��������Ϊa2����a1+a2= ��
��3������1���б���ס��4����֮�͵���76ʱ��x��ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�Ͷ��ڴ���������ij�̳���ƵĴ�������£���һ�����������������4����ͬ��С�����Ϸֱ������0Ԫ������10Ԫ������20Ԫ������50Ԫ�����������涨���ڱ��̳�ͬһ���ڣ��˿�ÿ������300Ԫ���Ϳ������������Ⱥ�����������һ�������Żأ����̳�������С��������ĺͷ�����ȼ۸�Ĺ���ȯ������ȯ�����ڱ��̳����ѣ�ij�˿պ�����300Ԫ��
��1���ù˿�����ɵõ�________Ԫ����ȯ��
��2�������û���״ͼ���б��ķ���������ù˿�����ù���ȯ�Ľ�����50Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
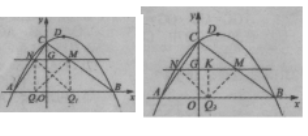
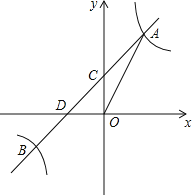
����Ŀ����ͼ������������![]() ��ͼ����һ�κ���y=kx+b��ͼ���ڵ�A��B����A��B�ĺ�����ֱ�Ϊ1����2��һ�κ���ͼ����y��Ľ��ڵ�C����x�ύ�ڵ�D��
��ͼ����һ�κ���y=kx+b��ͼ���ڵ�A��B����A��B�ĺ�����ֱ�Ϊ1����2��һ�κ���ͼ����y��Ľ��ڵ�C����x�ύ�ڵ�D��
��1����һ�κ����Ľ���ʽ��
��2���ڵ������ķ�����ͼ�����Ƿ����һ����P��ʹ��S��ODP=2S��OCA�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε����߳��ֱ���2��4��������߳�Ϊ�� ��
A.2B.4C.2��4D.3��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ε����߳��ֱ�Ϊ6��8��10�����������������ϵ����߳�Ϊ�� ��
A.3.6
B.4
C.4.8
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������Ա��ϰ��ֱ���۷��ܣ��������߳�������ǰ�������������ؼ������������ļ�¼����(��λ��m)����5����3����10����8����6����12����10.
(1)������������У�����Աһ�����˶����ף�
(2)�����������֪ʶ���з������ش�����Ա�뿪��������Զ�Ƕ����ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com