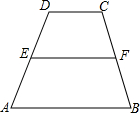
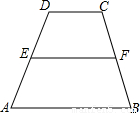
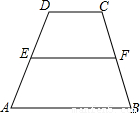
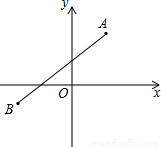
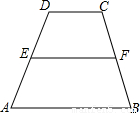
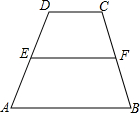
【探究】证明:过点F作GH∥AD,交AB于H,交DC的延长线于点G,

∵AH∥EF∥DG,AD∥GH,
∴四边形AHFE和四边形DEFG都是平行四边形,
∴FH=AE,FG=DE,
∵AE=DE,
∴FG=FH,
∵AB∥DG,
∴∠G=∠FHB,∠GCF=∠B,
∴△CFG≌△BFH,
∴FC=FB;
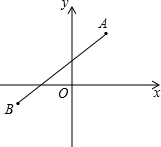
【知识应用】过点C作CM⊥x轴于点M,过点A作AN⊥x轴于点N,过点B作BP⊥x轴于点P,
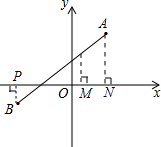
则点P的坐标为(x
2,0),点N的坐标为(x
1,0),
由探究的结论可知,MN=MP,
∴点M的坐标为(
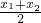
,0),
∴点C的横坐标为
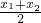
,
同理可求点C的纵坐标为
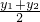
,
∴点C的坐标为(
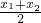
,
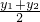
).
【知识拓展】
①当AB是平行四边形一条边,且点C在x轴的正半轴时,AD与BC互相平分,
设点C的坐标为(a,0),点D的坐标为(0,y)
由上面的结论可知:-6+a=4+0,-1+0=5+b,
∴a=10,b=-6,
∴此时点C的坐标为(10,0),点D的坐标为(0,-6),
②同理,当AB是平行四边形一条边,且点C在x轴的负半轴时,求得点C的坐标为(-10,0),点D的坐标为(0,6),
③当AB是对角线时点C的坐标为(-2,0),点D的坐标为(0,4).
分析:【探究】:过点F作GH∥AD,交AB于H,交DC的延长线于点G,求证△CFG≌△BFH即可;
【知识应用】:分别过A、B、C、三点作x轴的垂线,由A、B的坐标,进而即可求解点C的坐标;
【知识拓展】:由于点C、D的位置不确定,也即AB可能是平行四边形的边长,亦有可能是其对角线,所以应分几种情况:
即①当AB是平行四边形一条边,且点C在x轴的正半轴时,则AD与BC互相平分;
②当AB是平行四边形一条边,且点C在x轴的负半轴时,又是一种情况;
③当AB是对角线时,所以应分开来分别求解.
点评:本题主要考查了平行线的性质以及平行四边形的判定及性质和坐标问题,应在理解的基础上熟练求解.

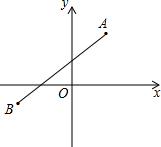

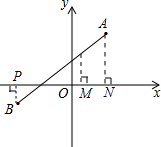
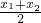 ,0),
,0),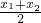 ,
,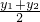 ,
,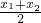 ,
,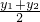 ).
).