
【题目】在![]() 中,点
中,点![]() 为
为![]() 上一点,点
上一点,点![]() 为
为![]() 上一点,且
上一点,且![]() .
.
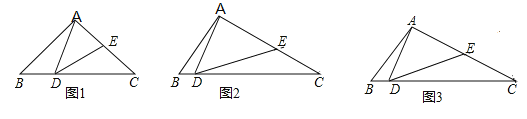
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,求证:
,求证:![]() ;
;
(3) 如图3,在(2)的条件下,若![]() ,且
,且![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)AB=![]() .
.
【解析】
(1)证明△ABD∽△DCE即可解决问题.
(2)如图2中,作CH∥AD交DE的延长线于H.首先证明CE=CH,再证明△BAD∽△HDC即可解决问题.
(3)如图3中,作CH∥AD交DE的延长线于H,作CG⊥EH于G.证明△ECH是等腰直角三角形,解直角三角形求出CD,DH,AD,再利用相似三角形的性质即可解决问题.
(1)证明:如图1中,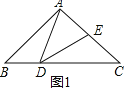
∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠DAB=∠ADE+∠EDC,∠ADE=∠B,
∴∠EDC=∠BAD,
∴△ABD∽△DCE,
∴![]() ,
,
∴![]() .
.
(2)证明:如图2中,作CH∥AD交DE的延长线于H.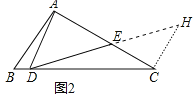
∵AD=AE,
∴∠ADE=∠AED,
∵AD∥CH,
∴∠H=∠ADE,
∵∠AED=∠CEH,
∴∠H=∠CEH,
∴CE=CH,
∵∠ADE=∠B,∠ADE=∠H,
∴∠B=∠H,
∵∠HDC=∠BAD,
∴△BAD∽△HDC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)解:如图3中,作CH∥AD交DE的延长线于H,作CG⊥EH于G.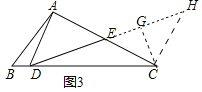
∵∠DAC=90°,AD=AE,
∴∠ADE=∠AED=∠H=∠CEH=45°,
∴EC=CH=4,∠ECH=90°,
∵CG⊥EH,
∴EH=4![]() ,EG=CG=GH=2
,EG=CG=GH=2![]() ,
,
∵sin∠CDE=![]() ,
,
∴CD=2![]() ,
,
∴DE=EG=2![]() ,DH=6
,DH=6![]() ,
,
∴AD=DE=2,
∵△BAD∽△HDC,
∴![]() ,
,
∴![]() ,
,
∴AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
人类会作圆并且真正了解圆的性质是在2000多年前,由我国的墨子给出圆的概念:“一中同长也.”.意思说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下的定义要早100年.与圆有关的定理有很多,弦切角定理就是其中之一.
我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
证明:如图①,AB与⊙O相切于点A.当圆心O在弦AC上时,容易得到∠CAB=90°,所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数.
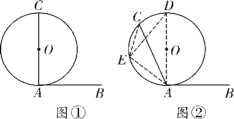
如图②,AB与⊙O相切于点A,当圆心O在∠BAC的内部时,过点A作直径AD交⊙O于点D,在![]() 上任取一点E,连接EC,ED,EA,则∠CED=∠CAD.
上任取一点E,连接EC,ED,EA,则∠CED=∠CAD.
…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
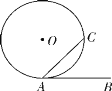
(2)如图③,AB与⊙O相切于点A.当圆心O在∠BAC的外部时,请写出弦切角定理的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
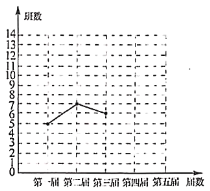
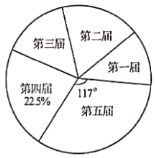
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
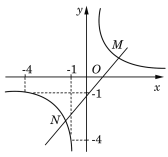
【题目】如图是反比例函数y=![]() 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.
(1)求该反比例函数的表达式;
(2)若点M,N分别在该反比例函数的两支图象上,请指出什么情况下线段MN最短(不需要证明),并注出线段MN长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正三角形ABC中,点D、E分别在AC、AB上,且![]() ,AE=BE,则有( )
,AE=BE,则有( )
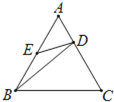
A.△AED∽△BEDB.△AED∽△CBD
C.△AED∽△ABDD.△BAD∽△BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
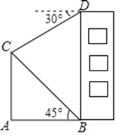
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC=2,AB=AC,点D为![]() 上的动点,且cos∠ABC=
上的动点,且cos∠ABC=![]() .
.
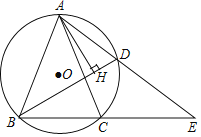
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
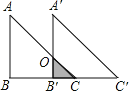
【题目】如图所示,已知Rt△ABC中,∠B=90°,BC=4,AB=4,现将△ABC沿BC方向平移到△A′B′C′的位置.若平移的距离为3,则△ABC与△A′B′C′重叠部分的阴影面积为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com