
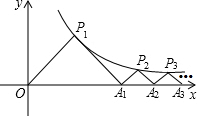
 如图△P1OA1,△P2A1A2,△P3A2A3,…,△P2015A2014A2015是等腰直角三角形,点P1,P2,P3,…都在函数$y=\frac{4}{x}$(x>0)x的图象上,斜边OA1,A1A2,A2A3,…A2014A2015都在x轴上,则A2015的坐标为(4$\sqrt{2015}$,0).
如图△P1OA1,△P2A1A2,△P3A2A3,…,△P2015A2014A2015是等腰直角三角形,点P1,P2,P3,…都在函数$y=\frac{4}{x}$(x>0)x的图象上,斜边OA1,A1A2,A2A3,…A2014A2015都在x轴上,则A2015的坐标为(4$\sqrt{2015}$,0). 分析 首先根据等腰直角三角形的性质,知点P1的横、纵坐标相等,再结合双曲线的解析式得到点P1的坐标是(2,2),则根据等腰三角形的三线合一求得点A1的坐标;同样根据等腰直角三角形的性质、点A1的坐标和双曲线的解析式求得A2点的坐标.根据A1、A2点的坐标特征即可推而广之得到An点的坐标.
解答 解:(1)可设点P1(x,y),
根据等腰直角三角形的性质可得:x=y,
又∵$y=\frac{4}{x}$,
则x2=4,
∴x=±2(负值舍去),
再根据等腰三角形的三线合一,得A1的坐标是(4,0),
设点P2的坐标是(4+y,y),
又∵$y=\frac{4}{x}$,则y(4+y)=4,即y2+4y-4=0
解得,y1=-2+2$\sqrt{2}$,y2=-2-2$\sqrt{2}$,
∵y>0,
∴y=2$\sqrt{2}$-2,
再根据等腰三角形的三线合一,得A2的坐标是(4$\sqrt{2}$,0);
同理得到:点A3的坐标是(4$\sqrt{3}$,0),
…
则An点的坐标是(4$\sqrt{n}$,0).
∴A2015的坐标为 (4$\sqrt{2015}$,0).
故答案是:(4$\sqrt{2015}$,0).
点评 本题考查了反比例函数的综合应用,解决此题的关键是要根据等腰直角三角形的性质以及反比例函数的解析式进行求解.


科目:初中数学 来源: 题型:解答题
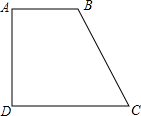 如图,在四边形ABCD中,AB∥CD,AB=12,BC=17,CD=20,AD=15.
如图,在四边形ABCD中,AB∥CD,AB=12,BC=17,CD=20,AD=15.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记PA=x,点D到直线PA的距离为y,则y关于x的函数解析式是( )
如图,矩形ABCD中,AB=3,BC=4,动点P从B点出发,在BC上移动至点C停止.记PA=x,点D到直线PA的距离为y,则y关于x的函数解析式是( )| A. | y=12x | B. | $y=\frac{12}{x}$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 利用某地七月份的日平均气温估计当地全年的日平均气温 | |
| B. | 为了解我国居民的年平均阅读时间,从大学生中随机抽取10万人进行抽查 | |
| C. | 调查某些七年级(1)班学生的身高;来估计该校全体学生的身高 | |
| D. | 为了了解一批洗衣粉的质量情况,从仓库中任意抽取100袋进行检验 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com