
【题目】定义:如图(1),若分别以△ABC的三边AC、BC、AB为边向三角形外侧作正方形ACDE、BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展
双叶正方形.
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2.
①如图(2),当∠ACB=90°时,求证:S1=S2;
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
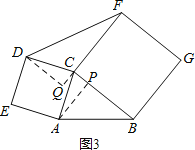
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF、△AEN、△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.

【答案】(1)①证明见解析;②S1=S2,理由见解析;(2)S的值发生变化,S的最大值是18.
【解析】分析:(1)由正方形的性质可以得出AC=DC,BC=FC,∠ACB=∠DCF=90°,就可以得出△ABC≌△DFC而得出结论;
(2)如图3,过点A作AP⊥BC于点P,过点D作DQ⊥FC交FC的延长线于点Q,通过证明△APC≌△DQC就有DQ=AP而得出结论;
(3)如图 1,根据(2)可以得出S=3S△ABC,要使S最大,就要使S△ABC最大,当∠AVB=90°时S△ABC最大,就可以求出结论
解析:(1)证明:如图1,∵正方形ACDE和正方形BCFG,
∴AC=DC,BC=FC,∠ACD=∠BCF=90°,
∵∠ACB=90°,∴∠DCF=90°,
∴∠ACB=∠DCF=90°.
在△ABC和△DFC中,
AC=DC
∠ACB=∠DCF
BC=FC
∴△ABC≌△DFC(SAS).
∴S△ABC=S△DFC,
∴S=S
(2)S1=S2,理由如下:
如图3,过点A作AP⊥BC于点P,过点D作DQ⊥FC交FC的延长线于点Q.
∴∠APC=∠DQC=90°.
∵四边形ACDE,BCFG均为正方形,
∴AC=CD,BC=CF,
∵∠ACP+∠ACQ=90°,∠DCQ+∠ACQ=90°.
∴∠ACP=∠DCQ.
在△APC和△DQC中
∠APC=∠DQC
∠ACP=∠DCQ
AC=DC
∴△APC≌△DQC(AAS),
∴AP=DQ.
∴BC×AP=DQ×FC,
∴S1=S2;
(3)由(2)得,S是△ABC面积的三倍,
要使S最大,只需三角形ABC的面积最大,
∴当△ABC是直角三角形,即∠ACB=90°时,S有最大值.
此时,S=3S△ABC=3×![]() =18
=18


科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
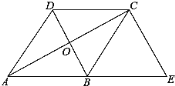
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com