
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时相向匀速行驶,当乙车到达
两地同时相向匀速行驶,当乙车到达![]() 地后,继续保持原速向远离
地后,继续保持原速向远离![]() 的方向行驶,而甲车到达
的方向行驶,而甲车到达![]() 地后,休息半小时后立即掉头,并以原速的
地后,休息半小时后立即掉头,并以原速的![]() 倍与乙车同向行驶,经过一段时间后,两车先后到达距
倍与乙车同向行驶,经过一段时间后,两车先后到达距![]() 地
地![]() 的
的![]() 地并停下来,设两车行驶的时间为
地并停下来,设两车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,
,![]() 与
与![]() 的函数关系如图,则当甲车从
的函数关系如图,则当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地__________
地__________![]() .
.
【答案】160
【解析】
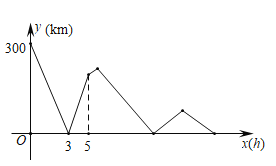
当x=0时,y=300,由此可得AB两地的距离为300km,由图象可知甲车到达B地用5小时,3小时后两车相遇,从而可求甲车的速度以及两车的速度之和,进而可得乙车的速度,再根据乙行驶5.5小时后,甲车从B地掉头追乙车,根据速度差可求出追乙车所用的时间,然后即可求解.
解:由图象可得:当x=0时,y=300,
∴AB=300千米,
∴甲车的速度=300÷5=60千米/小时,
又∵300÷3=100千米/小时,
∴乙车的速度=10060=40千米/小时,
∴当甲车从B地掉头开始追乙车时,乙车行驶的距离为40×5.5=220km,
∴甲车从B地掉头到追上乙车用的时间为:220÷(60×![]() -40)=5.5小时,
-40)=5.5小时,
∴当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地600-40×(5.5+5.5)=160km,
地600-40×(5.5+5.5)=160km,
故答案为:160.


科目:初中数学 来源: 题型:
【题目】等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连结CQ,设AP为x,△CPQ的面积为y,则y关于x的函数关系的图象大致是( )
A.  B.
B. 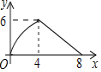 C.
C. 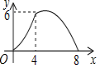 D.
D. 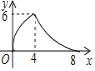
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣x+b分别与x轴,y轴交于A(6,0),B两点,过点B的另一直线交x轴的负半轴于点C,且OB:OC=3:1
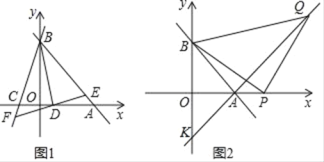
(1)求直线BC的解析式;
(2)直线y=ax﹣a(a≠0)交AB于点E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使S△BDE=S△BDF?若存在,求出a的值;若不存在,请说明理由;
(3)如图2,点P为A点右侧x轴上一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角三角形△BPQ,连接QA并延长交y轴于点K.当P点运动时,K点的位置是否发生变化?若不变,求出它的坐标;如果会发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的10×5网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点B按下列步骤移动第一步:点B绕点A逆时针旋转180°得到点B1;第二步:点B1绕点D逆时针旋转90°得到点B2;第三步:点B2绕点C逆时针旋转90°回到点B
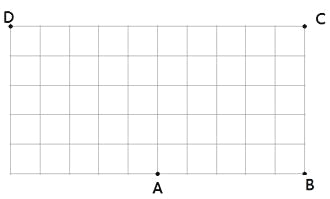
(1)请用圆规画出点B→B1→B2→B经过的路径;
(2)所画图形是_______图形;
(3)求所画图形的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且分别交
且分别交![]() 轴负半轴、直线
轴负半轴、直线![]() 于点
于点![]() 、
、![]() ,
,![]() .
.
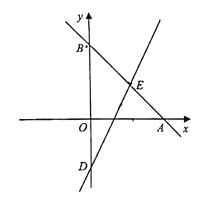
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)若点![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
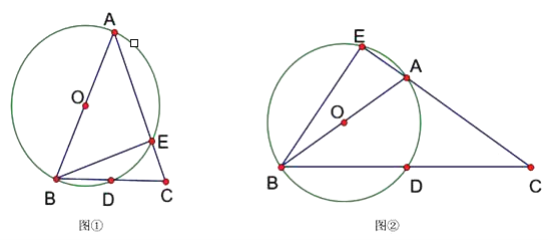
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)
甲:5、6、7、9、8
乙:8、4、8、6、9
(1)分别计算这两组数据的平均数和方差;
(2)根据测试成绩,你认为选派哪一名选手参赛更好些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
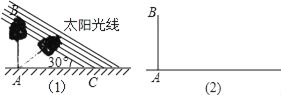
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com