
���� ��1�����������г�����ʽ��
��2�������ܷ���=����A�ij���������A��һ�����ķ���+�ҵ���A�ij��������ҵ�A��һ�����ķ��ã�ͬ����������ҵ��ܷ��ã�
��3�����ݵ�����ϵ�����˷�=900Ԫ���г�������⼴�ɣ�
��� �⣺��1�����Ӽײֿ����A��ũ�ó�x������ײֿ����B��ũ�ó���12-x������A����10���������Ҳֿ����A��ũ�ó���10-x�������Ҳֿ����B��ũ�ó���x-4������
��2����A���ܷ���=40x+30��10-x��=10x+300��
��B���ܷ���=80��12-x��+50��x-4��=760-30x��
�ʹ�˾�Ӽס��������ֿ����ũ�ó���A��B��������Ҫ�����˷�Ϊ��10x+300+760-30x=-20x+1060��
��3����������
-20x+1060=900��
���x=8��
�𣺴Ӽײֿ����A��ũ�ó�������
�ʴ�Ϊ����12-x������10-x������x-4����
���� ���⿼����һԪһ�η��̵�Ӧ�ã�������������������Ӧ���⣬������������Ϣ��ʹѧ�����еظ��ܵ�����ѧ��Դ����������鵽��ѧ�ġ������ԡ���������������ˡ��¿γ̱����ġ������龰-����ģ��-���͡�Ӧ�ú���չ������ѧѧϰģʽ��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �۳����������� | 7 | 6 | 3 | 5 | 4 | 5 |
| �ۼۣ�Ԫ�� | +3 | +2 | +1 | 0 | -1 | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
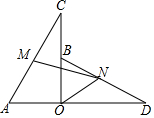 ��ͼ��OA=OB��OC=OD����AOB=��COD=90�㣬M��N�ֱ�ΪAC��BD���е㣬����MN��ON����֤����MNO=45�㣮
��ͼ��OA=OB��OC=OD����AOB=��COD=90�㣬M��N�ֱ�ΪAC��BD���е㣬����MN��ON����֤����MNO=45�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com