练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

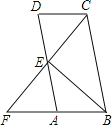
    【题目】如图，已知平行四边形ABCD中，E为AD中点，CE延长线交BA延长线于点F．

    （1）求证：CD=AF；

    （2）若BC=2CD，求证：∠F=∠BCF

    【答案】（1）证明见解析；（2）证明见解析.

    【解析】

    （1）CD和AF分别在△DCE和△AFE中，要证它们相等，只需证△DCE≌△AFE，根据平行四边形的性质及E为AD中点可证．
    （2）在平行四边形中，对边相等，由（1）的结论可证昨BF=BC，根据等边对等角可证．

    证明：（1）∵四边形ABCD是平行四边形，
    ∴AB∥DC．
    ∴∠DCE=∠AFE．
    ∵E是AD的中点，
    ∴DE=AE．
    在△DCE和△AFE中

    ，
    ∴△DCE≌△AFE．
    ∴CD=AF．

    （2）由（1）得CD=AF，
    ∵AB=CD，
    ∴BF=AF+AB=2CD．
    ∵BC=2CD，
    ∴BF=BC．
    ∴∠F=∠BCF．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，等腰直角三角形ABC位于第一象限，AB=AC=2，直角顶点A在直线y=x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线(k≠0)与△ABC有交点，则k的取值范围是（ ）

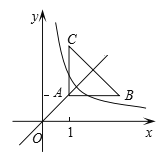
    A. 1≤k≤4 B. 1≤k＜4 C. 1＜k＜2 D. 1≤k≤3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1位同学植树的棵数不到8棵．若设同学人数为x人，植树的棵数为（7x+9）棵，下列各项能准确的求出同学人数与种植的树木的数量的是（　　）

    A. 7x+9≤8+9（x﹣1） B. 7x+9≥9（x﹣1）

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

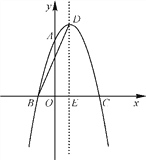
    【题目】如图，抛物线y＝ax2＋2x＋c经过点A(0，3)，B(－1，0)，请回答下列问题：

    (1)求抛物线对应的二次函数的表达式；

    (2)抛物线的顶点为D，对称轴与x轴交于点E，连接BD，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小张同学在计算时，将“”错看成了“”，得出的结果是．

    (1)请你求出这道题的正确结果；

    (2)试探索：当字母、满足什么关系时，(1)中的结果与字母的取值无关．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在A地到B地的快速通道某隧道建设，将由甲，乙两个工程队共同施工完成，据调查得知：甲，乙两队单独完成这项上程所需天数之比为4：5，若先由甲，乙两队合作40天，剩下的工程再乙队做10天完成，

    （1）求甲．乙两队单独完成这取工程各需多少天？

    （2）若此项工程由甲队做m天，乙队n天完成，

    ①请用含m的式子表示n；

    ②已知甲队每天的施工费为15万元，乙队每天的施工费用为10万元，若工程预算的总费用不超过1150万元，甲队工作的天数与乙队工作的天数之和不超过90天．请问甲、乙两队各工作多少天，完成此项工程总费用最少？最少费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+1经过A(-1，0)，B(1，1)两点．

    (1)求该抛物线的解析式；

    (2)阅读理解：

    在同一平面直角坐标系中，直线l1：y=k1x+b1(k1，b1为常数，且k1≠0)，直线l2：y=k2x+b2(k2，b2为常数，且k2≠0)，若l1⊥l2，则k1·k2=-1．

    解决问题：

    ①若直线y=3x-1与直线y=mx+2互相垂直，求m的值；

    ②是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由；

    (3)M是抛物线上一动点，且在直线AB的上方(不与A，B重合)，求点M到直线AB的距离的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠MAN＝15°，AB＝BC＝CD＝DE＝EF，则∠FEM＝________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一副直角三角板（其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°）

    （1）如图①放置，AB⊥AD,∠CAE=_______，BC与AD的位置关系是__________；

    （2）在（1）的基础上，再拿一个30°,60°,90°的直角三角板，如图②放置，将AC′边和AD边重合， AE是∠CAB′的角平分线吗，如果是，请加以说明，如果不是，请说明理由．

    （3）根据（1）（2）的计算，请解决下列问题：

    如图③∠BAD=90°，∠BAC=∠FAD= （是锐角），将一个45°,45°,90°直角三角板的一直角边与AD边重合，锐角顶点A与∠BAD的顶点重合，AE是∠CAF的角平分线吗？如果是，请加以说明，如果不是，请说明理由．

    查看答案和解析>>

    同步练习册答案