
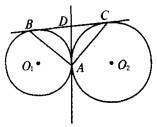
(1)求证:AB⊥AC;
(2)如图,若⊙O1与⊙O2外离时,连心线O1O2与⊙O1和⊙O2相交于M、N,BM、CN的延长线交于点A,则BA与CA是否垂直?请证明你的结论.
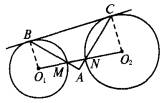
(3)若将上图中的⊙O1向右移动,使⊙O1与⊙O2相交(如下图),是否还有与(2)相应的结论?请画出相应的图形,并说明理由.
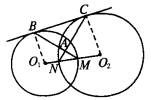
| (1)证明:过点A作⊙O1与⊙O2的内公切线AD交BC于D.因为BC是两圆的公切线,切点为B、C,所以DA=DB=DC,所以AC⊥AB.
(2)AB⊥AC成立. 证明:连结O1B、O2C. ∵ BC为⊙O1与⊙O2的外公切线,∴ O1B⊥BC,O2C⊥BC. ∴ O1B∥O2C.∴ ∠O1+∠O2=180°. 又∵ ∠CBA= ∴ ∠CBA+∠BCA= ∴ AB⊥AC. (3)结论仍成立,即AB⊥AC. 证明:连结O1B、O2C,则有O1B⊥BC,O2C⊥BC. ∴ O1B∥O2C.∴ ∠O1+∠O2=180°. 又∵ ∠CBA= ∴ ∠CBA+∠BCA= ∴ AB⊥AC
|
| 本题是圆的平移结论不变问题.解决问题的方法:(1)是根据特殊的位置关系,采用特殊的证法,实质上(2)、(3)的证法也适用于(1).解(3)的关键是准确画出图形,找准对应点.本题有“三不变”:结论不变,辅助线连法不变,证题方法不变.
|


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
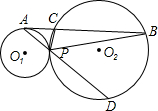 线AP交圆O2于点D,连接DC、PC.
线AP交圆O2于点D,连接DC、PC.| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、我们曾经证过《几何》第三册第145页练习第2题,即:
23、我们曾经证过《几何》第三册第145页练习第2题,即:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12 |
| 5 |
| 3 |
| 4 |
| 12 |
| 5 |
| 1 |
| CD |
| 1 |
| BE |
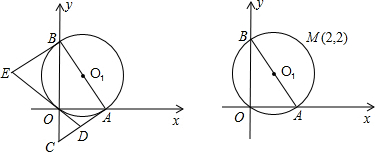 d,试判断d+AB的值是否会发生变化,若不变,求出其值;若变化,求其变化的范围.
d,试判断d+AB的值是否会发生变化,若不变,求出其值;若变化,求其变化的范围.查看答案和解析>>
科目:初中数学 来源:2011年广西省春季学期期中水平测试卷七年级数学 题型:填空题
如图6,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com