
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 7 | 10 |
| 汽车运费(元/辆) | 300 | 400 | 500 |
| A. | 6400元 | B. | 6500元 | C. | 6600元 | D. | 6700元 |
分析 设甲车有a辆,乙车有b辆,则丙车有(15-a-b)辆,列出等式.
解答 解:设甲车有a辆,乙车有b辆,则丙车有(15-a-b)辆,由题意得
5a+7b+10(15-a-b)=120,
化简得:5a+3b=30,
即a=6-$\frac{3}{5}$b,
∵a、b、15-a-b均为正整数,
∴b只能等于5,从而a=3,15-a-b=7,
∴甲车3辆,乙车5辆,丙车7辆,
∴需运费300×3+400×5+500×7=6400(元).
答:甲车3辆,乙车5辆,丙车7辆,需运费6400元.
故选:A.
点评 本题考查二元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.利用整体思想和未知数的实际意义通过筛选法可得到未知数的具体解,这种方法要掌握.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
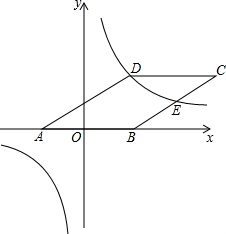 如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D,求该反比例函数的解析式.
如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D,求该反比例函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E、F分别为平行四边形ABCD中AB、CD的中点,BG⊥AF于G,
如图,E、F分别为平行四边形ABCD中AB、CD的中点,BG⊥AF于G,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,你能求出CD的长吗?
如图所示,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,你能求出CD的长吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com