
 如图,正方形ABCD中,AD=8,E是对角线AC的中点,动点P从点A出发,沿AB方向以每秒1个单位的速度向终点B运动,同时动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,再沿CD方向向终点D运动,连接EP,EQ,以EP、EQ为邻边作?PEQF,设点P运动的时间为t秒(t>0)
如图,正方形ABCD中,AD=8,E是对角线AC的中点,动点P从点A出发,沿AB方向以每秒1个单位的速度向终点B运动,同时动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,再沿CD方向向终点D运动,连接EP,EQ,以EP、EQ为邻边作?PEQF,设点P运动的时间为t秒(t>0)分析 (1)作EM⊥AB于M,由正方形的性质和已知条件得出AB=BC=CD=AD=8,AM=BM=$\frac{1}{2}$AB=4,得出EM是△ABC的中位线,由三角形中位线定理得出EM=$\frac{1}{2}$BC=4,当t=1时,AP=1,求出PM=AM-AP=3,再由勾股定理求出PE即可;
(2)由平行四边形的性质得出PF=EQ,PF∥EQ,当点F恰好落在线段AB上时,得出EQ⊥BC,Q为BC的中点,得出EQ是△ABC的中位线,由三角形中位线定理得出EQ=$\frac{1}{2}$AB=4,求出PF=4,AP=2,即可求出BF的长;
(3)由菱形的性质得出PE=PQ,分四种情况:①当0<t≤2时,作EM⊥AB于M,EN⊥BC于N;②当2<t≤4时;③当4<t≤6时,作EM⊥AB于M,EN⊥BC于N;④当6<t≤8时;分别由勾股定理得出方程,解方程即可.
解答 解:(1)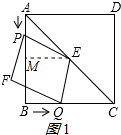 作EM⊥AB于M,如图1所示:
作EM⊥AB于M,如图1所示:
∵四边形ABCD是正方形,E是对角线AC的中点,
∴AB=BC=CD=AD=8,AM=BM=$\frac{1}{2}$AB=4,
∴EM是△ABC的中位线,
∴EM=$\frac{1}{2}$BC=4,
当t=1时,AP=1,
∴PM=AM-AP=3,
∴PE=$\sqrt{P{M}^{2}+E{M}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)∵四边形PEQF是平行四边形,
∴PF=EQ,PF∥EQ,
当点F恰好落在线段AB上时,PF⊥BC,
∴EQ⊥BC,
∴Q为BC的中点,
∴EQ是△ABC的中位线,BQ=$\frac{1}{2}$BC=4,
∴EQ=$\frac{1}{2}$AB=4,
∴PF=4,
∵动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,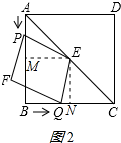
∴t=4÷2=2,
∴AP=2,
∴BF=AB-AP=PF=2;
(3)当?PEQF为菱形时,PE=PQ,分四种情况:
①当0<t≤2时,作EM⊥AB于M,EN⊥BC于N,如图2所示:
∵PE2=PM2+EM2,EQ2=QN2+EN2,
∴(4-t)2+42=(4-2t)2+42,
解得:t=0(舍去),或t=$\frac{8}{3}$(舍去);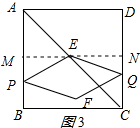
②当2<t≤4时,
同①得:(4-t)2+42=(2t-4)2+42,
解得:t=0(舍去),或t=$\frac{8}{3}$,
∴t=$\frac{8}{3}$;
③当4<t≤6时,作EM⊥AB于M,EN⊥BC于N,如图3所示:
∵PE2=PM2+EM2,EQ2=QN2+EN2,
∴(t-4)2+42=(12-2t)2+42,
解得:t=$\frac{16}{3}$,或t=8(舍去),
∴t=$\frac{16}{3}$;
④当6<t≤8时,
同③得:(t-4)2+42=(2t-12)2+42,
解得:t=$\frac{16}{3}$(舍去),或t=8(舍去);
综上所述:在整个运动过程中,当?PEQF为菱形时,t的值为$\frac{8}{3}$s或$\frac{16}{3}$s.
点评 本题是四边形综合题目,考查了正方形的性质、勾股定理、平行四边形的性质、三角形中位线定理、菱形的性质等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线进行分类讨论,运用勾股定理得出方程才能得出结果.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
| 尺码(单位:cm) | 人数 |
| 140≤x<150 | 7 |
| 150≤x<160 | 30 |
| 160≤x<170 | 10 |
| 170≤x<180 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
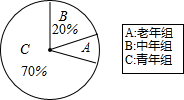 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=$\frac{1}{n}$AD(n为大于1的整数),作对角线BD的垂直平分线分别交AD,BC于点E,F,EF与BD的交点为O,连接BE和DF.
如图,矩形ABCD中,AB=$\frac{1}{n}$AD(n为大于1的整数),作对角线BD的垂直平分线分别交AD,BC于点E,F,EF与BD的交点为O,连接BE和DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AD是中线,DE⊥BC交AB于E,AH∥DE交BC于H,且∠DAH=∠CAH,连接CE交AD于F,交AH于G.下列结论:①△AEF∽△CEA;②FH∥AC;③若CE⊥AB,则tan∠BAC=2;④若四边形AEDG是菱形,则∠ACB=60°.其中正确的是( )
如图,在△ABC中,AD是中线,DE⊥BC交AB于E,AH∥DE交BC于H,且∠DAH=∠CAH,连接CE交AD于F,交AH于G.下列结论:①△AEF∽△CEA;②FH∥AC;③若CE⊥AB,则tan∠BAC=2;④若四边形AEDG是菱形,则∠ACB=60°.其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①② | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3>b-3 | B. | -2+a>-2+b | C. | $\frac{a}{5}$$>\frac{b}{5}$ | D. | -2a>-2b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com