
分析 ①把m=2代入,利用配方法求顶点坐标;
②利用对称轴和增减性的性质可知,对称轴一定是x=1的右侧;
③根据平移原则:左⇒+,右⇒一,得出解析式,并利用最值列式;
④根据已知先求m的值,写出解析式,把x=2016代入求y.
解答 解:①当m=2时,二次函数为y=x2-4x+3=(x-2)2-1,
∵a=1>0,
∴当x=2时,y有最小值为-1;故①正确;
②如果当x≤1时y随x的增大而减小,则-$\frac{-2m}{2×1}$=m≥1;故②错误;
③y=x2-2mx+3=(x-m)2-m2+3,
将它的图象向左平移3个单位后的函数:y=(x-m+3)2-m2+3,
则-m2+3=-9,m=±2$\sqrt{3}$,
∵m>0,
∴m=2$\sqrt{3}$,故③正确;
④由当x=1时的函数值与x=2015时的函数值相等得:12-2m+3=20152-4030m+3,m=1008,
∴当x=2016时,y=20162-2×2016×1008+3=3,故④正确;
故答案为:①③④.
点评 本题考查了二次函数的性质,是常考题型;要注意每一个条件都只能在本选项中运用,各选项中根据自己的已知条件求出相应的m的值.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
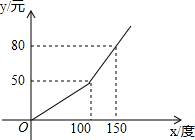 为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量.
为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
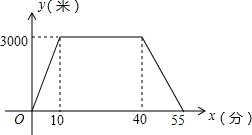 小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )
小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )| A. | 小刘家与超市相距3000米 | |
| B. | 小刘去超市途中的速度是300米/分 | |
| C. | 小刘在超市逗留了30分钟 | |
| D. | 小刘从超市返回家比从家里去超市的速度快 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
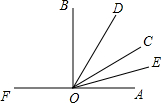 如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
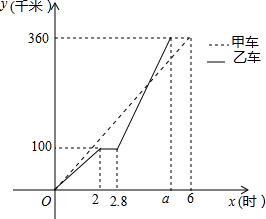 甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,
甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com