
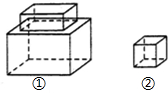
 某玩具加工厂要制造如图所示的两种形状的玩具配件,其中,配件①是由大、小两个长方体构成的,大长方体的长、宽、高分别为:$\frac{5}{2}$a、2a、$\frac{3}{2}$a,小长方体的长、宽、高分别为:2a、a、$\frac{a}{2}$;配件②是一个正方体,其边长为a
某玩具加工厂要制造如图所示的两种形状的玩具配件,其中,配件①是由大、小两个长方体构成的,大长方体的长、宽、高分别为:$\frac{5}{2}$a、2a、$\frac{3}{2}$a,小长方体的长、宽、高分别为:2a、a、$\frac{a}{2}$;配件②是一个正方体,其边长为a分析 (1)先算出两个长方形的体积,再相加,即可得出配件①的体积,求出边长为a的正方形体积,即可得出配件②的体积;
(2)根据题意列出算式1000a3÷(2×$\frac{17}{2}$a3+a3)×30,求出即可.
解答 解:(1)生产配件①需要的原材料的体积是:$\frac{5}{2}$a•2a•$\frac{3}{2}$a+2a•a•$\frac{a}{2}$=$\frac{17}{2}$a3;
生产配件②需要的原材料的体积是:a•a•a=a3;
(2)根据题意得:1000a3÷(2×$\frac{17}{2}$a3+a3)×30=$\frac{5000}{3}$(元),
答:1000a3体积的这种原材料可使该厂最多获利$\frac{5000}{3}$元.
点评 本题考查了整式的混合运算,能根据题意列出算式是解此题的关键,用了转化思想.


科目:初中数学 来源: 题型:解答题
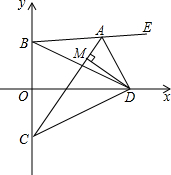 如图,在平面直角坐标系中,B(0,1),C(0,-1),D为x轴正半轴上一点,A为第一象限内一动点,且∠BAC=2∠BDO,DM⊥AC于M.
如图,在平面直角坐标系中,B(0,1),C(0,-1),D为x轴正半轴上一点,A为第一象限内一动点,且∠BAC=2∠BDO,DM⊥AC于M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.
如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.
有这样一个问题:探究函数y=x2-2$\sqrt{{x}^{2}}$的图象与性质.| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | n | 3 | 0 | -1 | 0 | -1 | 0 | 3 | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com