练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图①、②，解答下面各题：
    （1）图①中，∠AOB＝45°，点P在∠AOB内部，过点P作PE⊥OA，PF⊥OB，
    垂足分别为E、F，求∠EPF的度数.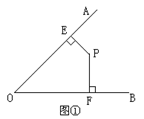

    （2）图②中，点P在∠AOB外部，过点P作PE⊥OA，PF⊥OB，垂足分别为E、F，那么∠P与∠O有什么关系.？为什么？

    略

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

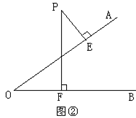
    科目：初中数学 来源： 题型：

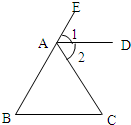
    23、已知，如图，∠BAE+∠AED=180°，∠1=∠2，那么∠M=∠N（下面是推理过程，请你填空．
    解∵∠BAE+∠AED=180°（已知）
    ∴
    AB
    ∥
    CD
    （同旁内角互补，两直线平行）
    ∴∠BAE=
    ∠AEC
    （两直线平行，内错角相等）
    又∵∠1=∠2
    ∴∠BAE-∠1=
    ∠AEC
    -
    ∠2

    即∠MAE=
    ∠AEN

    ∴
    AM
    ∥
    EN
    （内错角相等，两直线平行）
    ∴∠M=∠N（两直线平行，内错角相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    22、根据图形及题意填空，并在括号里写上理由．
    已知：如图，AD∥BC，AD平分∠EAC．
    试说明：∠B=∠C
    解：∵AD平分∠EAC（已知）
    ∴∠1=∠2（角平分线的定义）
    ∵AD∥BC（已知）
    ∴∠
    1
    =∠
    B
    （
    两直线平行，同位角相等
    ）
    ∠
    2
    =∠
    C
    （
    两直线平行，内错角相等
    ）
    ∴∠B=∠C．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    22、结合图形填空：
    已知，如图，∠BAE+∠AED=180°，∠M=∠N
    试说明：∠1=∠2
    解：∵∠BAE+∠AED=180°
    ∴
    AB
    ∥
    CD
    （同旁内角互补，两直线平行）
    ∴∠BAE=
    ∠AEC
    （两直线平行，内错角相等）
    又∵∠M=∠N （已知）
    ∴
    AN
    ∥
    ME
    （内错角相等，两直线平行）
    ∴∠NAE=
    ∠MEA
    （两直线平行，内错角相等）
    ∴∠BAE-∠NAE=
    ∠AEC
    -
    ∠MEA

    即∠1=∠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知，如图，方程组
    y=kx+b
    y=mx+n
    的解是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，AB∥DE，∠B=80°，∠D=140°，求∠BCD的度数．
    解：过C点作CF∥DE． （
    辅助线的作法
    辅助线的作法
    ）
    ∵AB∥DE．
    ∴AB∥
    CF
    CF
    ． （
    平行公理
    平行公理
    ）
    ∴∠B=∠
    BCF
    BCF
    ．  （
    两直线平行，内错角相等
    两直线平行，内错角相等
    ）
    ∠D+
    ∠DCF
    ∠DCF
    =180° （
    两直线平行，同旁内角互补
    两直线平行，同旁内角互补
    ）
    ∵∠B=80°∠D=140°
    ∴∠
    BCF
    BCF
    =
    80
    80
    °，∠
    DCF
    DCF
    =
    40
    40
    °．
    ∵∠BCD=∠
    BCF
    BCF
    -∠
    DCF
    DCF
    ．
    ∴∠BCD=
    40°
    40°
    ．

    查看答案和解析>>

    同步练习册答案