
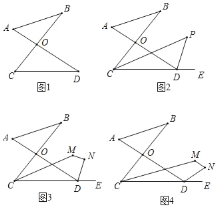
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЕФЭМаЮЮвУЧАбЫќГЦЮЊЁА8зжаЮЁБЃЌдђЁЯAЃЌЁЯBЃЌЁЯCЃЌЁЯDЫФИіНЧЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєЁЯBCDЃЌЁЯADEЕФНЧЦНЗжЯпCPЃЌDPНЛгкЕуPЃЌдђЁЯPгыЁЯAЃЌЁЯBЕФЪ§СПЙиЯЕЮЊЁЯPЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌCMЃЌDNЗжБ№ЦНЗжЁЯBCDЃЌЁЯADEЃЌЕБЁЯA+ЁЯBЃН80ЁуЪБЃЌЪдЧѓЁЯM+ЁЯNЕФЖШЪ§ЃЈЬсабЃКНтОіДЫЮЪЬтПЩвджБНгРћгУЩЯЪіНсТлЃЉЃЛ
ЃЈ4ЃЉШчЭМ4ЃЌШчЙћЁЯMCDЃН![]() ЁЯBCDЃЌЁЯNDEЃН
ЁЯBCDЃЌЁЯNDEЃН![]() ЁЯADEЃЌЕБЁЯA+ЁЯBЃНnЁуЪБЃЌЪдЧѓЁЯM+ЁЯNЕФЖШЪ§ЃЎ
ЁЯADEЃЌЕБЁЯA+ЁЯBЃНnЁуЪБЃЌЪдЧѓЁЯM+ЁЯNЕФЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЯA+ЁЯBЃНЁЯC+ЁЯDЃЛЃЈ2ЃЉ90ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉЃЛЃЈ3ЃЉЁЯCMN+ЁЯDNMЃН230ЁуЃЛЃЈ4ЃЉЁЯCMN+ЁЯDNMЃН240ЁуЉ
ЃЈЁЯA+ЁЯBЃЉЃЛЃЈ3ЃЉЁЯCMN+ЁЯDNMЃН230ЁуЃЛЃЈ4ЃЉЁЯCMN+ЁЯDNMЃН240ЁуЉ![]() nЁуЃЎ
nЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩШ§НЧаЮЕФФкНЧКЭОљЮЊ180ЁуМАЭМжаЁЯAOBКЭЁЯCODЮЊЖдЖЅНЧПЩжЊЁЯA+ЁЯBЃНЁЯC+ЁЯDЃЛ
ЃЈ2ЃЉЩшЁЯPCDЃНxЃЌЁЯADPЃНyЃЌгЩCPЃЌDPОљЮЊНЧЦНЗжЯпПЩЕУЁЯBCDЃН2xЃЌЁЯADEЃН2yЃЛдйгЩШ§НЧаЮЭтНЧКЭЖЈРэПЩЕУЁЯPЃНЁЯPDEЉЁЯPCDЃНyЉxЃЌЁЯCODЃНЁЯODEЉЁЯBCDЃН2yЉ2xЃЌдђПЩЧѓЕУЁЯCODЃН2ЁЯPЃЛгЩШ§НЧаЮФкНЧКЭЖЈРэвдМАЁЯCODКЭЁЯAOBЪЧЖдЖЅНЧПЩЕУЃЌЁЯCOD+ЁЯA+ЁЯBЃН180ЁуЃЌдйгУЁЯCODЃН2ЁЯPНјааЬцЛЛПЩЕУЁЯPЃН90ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉЃЛ
ЃЈЁЯA+ЁЯBЃЉЃЛ
ЃЈ3ЃЉбгГЄCMЁЂDNНЛгкЕуPЃЌгЩЩЯвЛЮЪНсТлПЩжЊЁЯPЃН90ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉЃЌНсКЯЬтИЩЫљИјЬѕМўвзЧѓЕУЁЯPЃН50ЁуЃЌгЩШ§НЧаЮФкНЧКЭЖЈРэПЩЕУЁЯPMN+ЁЯPNMЃН130ЁуЃЌдђЁЯM+ЁЯNЃН360Ёу-(ЁЯPMN+ЁЯPNM)=360ЁуЉ130ЁуЃН230ЁуЃЛ
ЃЈЁЯA+ЁЯBЃЉЃЌНсКЯЬтИЩЫљИјЬѕМўвзЧѓЕУЁЯPЃН50ЁуЃЌгЩШ§НЧаЮФкНЧКЭЖЈРэПЩЕУЁЯPMN+ЁЯPNMЃН130ЁуЃЌдђЁЯM+ЁЯNЃН360Ёу-(ЁЯPMN+ЁЯPNM)=360ЁуЉ130ЁуЃН230ЁуЃЛ
ЃЈ4ЃЉбгГЄCMЁЂDNНЛгкЕуPЃЌЩшЁЯPCDЃНxЃЌЁЯADPЃН2yЃЌгЩЁЯMCDЃН![]() ЁЯBCDЃЌЁЯNDEЃН
ЁЯBCDЃЌЁЯNDEЃН![]() ЁЯADEвзЕУЁЯNDEЃНyЃЌЁЯBCD=3xЃЌдйгЩШ§НЧаЮЭтНЧКЭЖЈРэвдМАФкНЧКЭЖЈРэвзЕУЁЯPЃНyЉxЃЌЁЯCODЃН3yЉ3xЃЌдђЁЯCODЃН3ЁЯPЃЛгЩШ§НЧаЮФкНЧКЭЖЈРэПЩЕУ3ЁЯP+ЁЯA+ЁЯBЃН180ЁуЃЌЬтИЩвбжЊЁЯA+ЁЯBЃНnЁуЃЌдђПЩжЊЁЯPЃН
ЁЯADEвзЕУЁЯNDEЃНyЃЌЁЯBCD=3xЃЌдйгЩШ§НЧаЮЭтНЧКЭЖЈРэвдМАФкНЧКЭЖЈРэвзЕУЁЯPЃНyЉxЃЌЁЯCODЃН3yЉ3xЃЌдђЁЯCODЃН3ЁЯPЃЛгЩШ§НЧаЮФкНЧКЭЖЈРэПЩЕУ3ЁЯP+ЁЯA+ЁЯBЃН180ЁуЃЌЬтИЩвбжЊЁЯA+ЁЯBЃНnЁуЃЌдђПЩжЊЁЯPЃН![]() ЃЌЭЌЩЯЮЪЁЯCMN+ЁЯDNMЃН360ЁуЉ(ЁЯPMN+ЁЯPNM)=360Ёу-ЃЈ120Ёу+
ЃЌЭЌЩЯЮЪЁЯCMN+ЁЯDNMЃН360ЁуЉ(ЁЯPMN+ЁЯPNM)=360Ёу-ЃЈ120Ёу+![]() ЃЉЃН240ЁуЉ
ЃЉЃН240ЁуЉ![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌдкЁїAOBжаЃЌЁЯA+ЁЯB+ЁЯAOBЃН180ЁуЃЌ
дкЁїCODжаЃЌЁЯC+ЁЯD+ЁЯCODЃН180ЁуЃЌ
ЁпЁЯAOBЃНЁЯCODЃЌ
ЁрЁЯA+ЁЯBЃНЁЯC+ЁЯDЃЛ
ЙЪД№АИЮЊЃКЁЯA+ЁЯBЃНЁЯC+ЁЯDЃЛ
ЃЈ2ЃЉЩшЁЯPCDЃНxЃЌЁЯADPЃНyЃЌ
ЁпCPЃЌDPЗжБ№ЦНЗжЁЯBCDЃЌЁЯADEЃЌ
ЁрЁЯBCDЃН2xЃЌЁЯADEЃН2yЃЌ
ЁпЁЯPЃНЁЯPDEЉЁЯPCDЃНyЉxЃЌ
ЁЯCODЃНЁЯODEЉЁЯBCDЃН2yЉ2xЃЌ
ЁрЁЯCODЃН2ЁЯPЃЌ
ЁпЁЯCOD+ЁЯA+ЁЯBЃН180ЁуЃЌ
Ёр2ЁЯP+ЁЯA+ЁЯBЃН180ЁуЃЌ
ЁрЁЯPЃН90ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉЃЛ
ЃЈЁЯA+ЁЯBЃЉЃЛ
ЙЪД№АИЮЊЃК90ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉЃЛ
ЃЈЁЯA+ЁЯBЃЉЃЛ
ЃЈ3ЃЉбгГЄCMЁЂDNНЛгкЕуPЃЌ
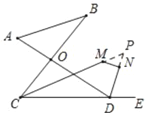
гЩЃЈ2ЃЉжЊЃКЁЯPЃН90ЁуЉ![]() ЃЈЁЯA+ЁЯBЃЉЃЌ
ЃЈЁЯA+ЁЯBЃЉЃЌ
ЁпЁЯA+ЁЯBЃН80ЁуЃЌ
ЁрЁЯPЃН50ЁуЃЌ
ЁрЁЯPMN+ЁЯPNMЃН130ЁуЃЌ
ЁрЁЯCMN+ЁЯDNMЃН360ЁуЉ130ЁуЃН230ЁуЃЛ
ЃЈ4ЃЉбгГЄCMЁЂDNНЛгкЕуPЃЌ

ЩшЁЯPCDЃНxЃЌЁЯADPЃН2yЃЌ
ЁпЁЯMCDЃН![]() ЁЯBCDЃЌЁЯNDEЃН
ЁЯBCDЃЌЁЯNDEЃН![]() ЁЯADEЃЌ
ЁЯADEЃЌ
ЁрЁЯNDEЃНyЃЌЁЯBCD=3xЃЌ
ЁрЁЯPЃНyЉxЃЌЁЯCODЃН3yЉ3xЃЌ
ЁрЁЯCODЃН3ЁЯPЃЌ
Ёр3ЁЯP+ЁЯA+ЁЯBЃН180ЁуЃЌ
ЁпЁЯA+ЁЯBЃНnЁуЃЌ
ЁрЁЯPЃН![]() ЃЌ
ЃЌ
ЁрЁЯPMN+ЁЯPNMЃН180ЁуЉ![]() ЃН120Ёу+
ЃН120Ёу+![]() ЃЌ
ЃЌ
ЁрЁЯCMN+ЁЯDNMЃН360ЁуЉЃЈ120Ёу+![]() ЃЉЃН240ЁуЉ
ЃЉЃН240ЁуЉ![]() ЃЎ
ЃЎ


 ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
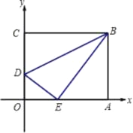
ЁОЬтФПЁПНЋвЛОиаЮжНЦЌOABCЗХдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊдЕуЃЌЕуAдкxжсЩЯЃЌЕуCдкyжсЩЯЃЌOA=10ЃЌOC=8ЃЌШчЭМдкOCБпЩЯШЁвЛЕуDЃЌНЋЁїBCDбиBDелЕўЃЌЪЙЕуCЧЁКУТфдкOAБпЩЯЃЌМЧзїEЕуЃЛ
ЃЈ1ЃЉЧѓЕуEЕФзјБъМАелКлDBЕФГЄЃЛ
ЃЈ2ЃЉдкxжсЩЯШЁСНЕуMЁЂNЃЈЕуMдкЕуNЕФзѓВрЃЉЃЌЧвMN=4.5ЃЌЧѓЪЙЫФБпаЮBDMNЕФжмГЄзюЖЬЕФЕуMЁЂЕуNЕФзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAB=ACЃЌFDЁЭBCгкDЃЌDEЁЭABгкEЃЌШєЁЯAFD=145ЁуЃЌдђЁЯEDF=ЖШЃЎ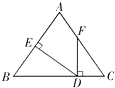
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаФГжабЇОйааЁАжаЙњУЮаЃдАКУЩљвєЁБИшЪжДѓШќЃЌИпЁЂГѕжаВПИљОнГѕШќГЩМЈЃЌИїбЁГі5УћбЁЪжзщГЩГѕжаДњБэЖгКЭИпжаДњБэЖгВЮМгбЇаЃОіШќЃЎСНИіЖгИїбЁГіЕФ5УћбЁЪжЕФОіШќГЩМЈШчЭМЫљЪОЃЎ

ЃЈ1ЃЉИљОнЭМЪОЬюаДЯТБэЃЛ
ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ | |
ГѕжаВП | 85 | ||
ИпжаВП | 85 | 100 |
ЃЈ2ЃЉНсКЯСНЖгГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§ЃЌЗжЮіФФИіЖгЕФОіШќГЩМЈНЯКУЃЛ
ЃЈ3ЃЉМЦЫуСНЖгОіШќГЩМЈЕФЗНВюВЂХаЖЯФФвЛИіДњБэЖгбЁЪжГЩМЈНЯЮЊЮШЖЈЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКвЛзщЪ§Онx1ЃЌx2ЃЌx3ЃЌx4ЃЌx5ЕФЦНОљЪ§ЪЧ2ЃЌЗНВюЪЧ![]() ЃЌФЧУДСэвЛзщЪ§Он3x1Љ2ЃЌ3x2Љ2ЃЌ3x3Љ2ЃЌ3x4Љ2ЃЌ3x5Љ2ЕФЦНОљЪ§КЭЗНВюЗжБ№ЪЧЃЈЁЁЁЁЃЉ
ЃЌФЧУДСэвЛзщЪ§Он3x1Љ2ЃЌ3x2Љ2ЃЌ3x3Љ2ЃЌ3x4Љ2ЃЌ3x5Љ2ЕФЦНОљЪ§КЭЗНВюЗжБ№ЪЧЃЈЁЁЁЁЃЉ
A. 2ЃЌ![]() B. 2ЃЌ1 C. 4ЃЌ
B. 2ЃЌ1 C. 4ЃЌ![]() D. 4ЃЌ3
D. 4ЃЌ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
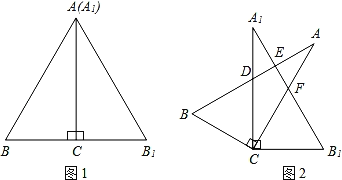
ЁОЬтФПЁПНЋСНПщШЋЕШЕФКЌ30ЁуНЧЕФжБНЧШ§НЧАтАДЭМ1ЕФЗНЪНЗХжУЃЌвбжЊЁЯBACЃНЁЯB1A1CЃН30ЁуЃЌABЃН2BCЃЎЙЬЖЈШ§НЧАхA1B1CЃЌШЛКѓНЋШ§НЧАхABCШЦЕуCЫГЪБеыЗНЯђа§зЊЃЈШчЭМ2ЫљЪОЃЉЃЌABгыA1CЁЂA1B1ЗжБ№НЛгкЕуDЁЂEЃЌACгыA1B1НЛгкЕуFЃЎИјГіЯТСаНсТлЃК
ЂйЕБа§зЊНЧЕШгк20ЁуЪБЃЌЁЯBCB1ЃНl60ЁуЃЛ
ЂкЕБа§зЊНЧЕШгк30ЁуЪБЃЌABгыA1B1ДЙжБЃЛ
ЂлЕБа§зЊНЧЕШгк45ЁуЪБЃЌABЁЮCB1ЃЛ
ЂмЕБABЁЮCB1ЪБЃЌЕуDЮЊA1CЕФжаЕуЃЎ
Цфжае§ШЗЕФЪЧ_____ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
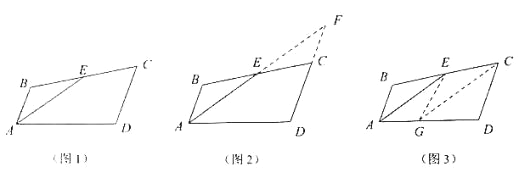
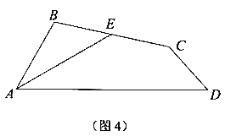
аЁУїгіЕНетбљвЛИіЮЪЬт:ШчЭМ 1,дкЫФБпаЮ ABCD жа,E ЪЧ BC ЕФжаЕу,AE ЪЧЁЯBAD ЕФЦНЗжЯп,ABЁЮDCЃЌЧѓжЄ:AD=AB+DC. аЁУїЗЂЯжвдЯТСНжжЗНЗЈ:
ЗНЗЈ 1:ШчЭМ 2,бгГЄ AEЁЂDC НЛгкЕу FЃЛ
ЗНЗЈ 2:ШчЭМ 3,дк AD ЩЯШЁвЛЕу G ЪЙ AG=AB,СЌНг EGЁЂCG.
(1)ИљОндФЖСВФСЯ,ШЮбЁвЛжжЗНЗЈ,жЄУїЃКAD=AB+DCЃЛ гУбЇЙ§ЕФжЊЪЖЛђВЮПМаЁУїЕФЗНЗЈ,НтОіЯТУцЕФЮЪЬт:
(2)ШчЭМ 4,дкЫФБпаЮ ABCD жа,AE ЪЧЁЯBAD ЕФЦНЗжЯп,E ЪЧ BC ЕФжаЕу,ЁЯBAD=60Ёу,ЁЯABC=180Ёу-![]() ЁЯBCDЃЌЧѓжЄ:CD=CE.
ЁЯBCDЃЌЧѓжЄ:CD=CE.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯA=60ЁуЃЌAC=6ЃЌНЋЁїABCШЦЕуCАДФцЪБеыЗНЯђа§зЊЕУЕНЁїA'B'C'ЃЌДЫЪБЕуA'ЧЁКУдкABБпЩЯЃЌдђЕуB'гыЕуBжЎМфЕФОрРыЮЊЃЈЁЁЁЁЃЉ
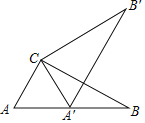
A. 12 B. 6 C. 6![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧрЩНЛЏЙЄГЇгыAЁЂBСНЕигаЙЋТЗЁЂЬњТЗЯрСЌЃЌетМвЙЄГЇДгAЕиЙКТђвЛХњУПЖж1000дЊЕФдСЯОЬњТЗ120kmКЭЙЋТЗ10kmдЫЛиЙЄГЇЃЌжЦГЩУПЖж8000дЊЕФВњЦЗОЬњТЗ110kmКЭЙЋТЗ20kmЯњЪлЕНBЕиЃЎвбжЊЬњТЗЕФдЫМлЮЊ1.2дЊ/ЃЈЖжЁЄЧЇУз)ЃЌЙЋТЗЕФдЫМлЮЊ1.5дЊ/(ЖжЁЄЧЇУз)ЃЌЧветСНДЮдЫЪфЙВжЇГіЬњТЗдЫЗб124800дЊЃЌЙЋТЗдЫЗб19500дЊЃЎ
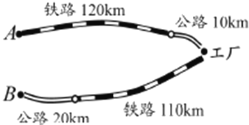
ЃЈ1ЃЉЩшдСЯжиxЖжЃЌВњЦЗжиyЖжЃЌИљОнЬтжаЪ§СПЙиЯЕЬюаДЯТБэ
дСЯxЖж | ВњЦЗyЖж | КЯМЦЃЈдЊЃЉ | |
ЬњТЗдЫЗб | 124800 | ||
ЙЋТЗдЫЗб | 19500 |
ИљОнЩЯБэСаЗНГЬзщЧѓдСЯКЭВњЦЗЕФжиСПЃЎ
ЃЈ2ЃЉетХњВњЦЗЕФЯњЪлПюБШдСЯЗбгыдЫЪфЗбЕФКЭЖрЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com