
【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
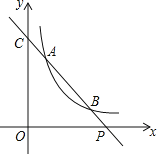
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
【答案】(1)P(4,O);(2)A(2,2),B(4,1);(3)![]() .
.
【解析】试题分析:(1)把A点坐标代入反比例函数解析式可求得k,进一步可求得B点坐标,再利用待定系数法可求得直线解析式,可求得P点坐标;
(2)过点A作AD∥x轴,交x轴于点D,利用△ACD∽△PCO,结合A、P、C的坐标可求得x1、y1之间的关系,结合AB=BP可表示出B点坐标,再结合A、B两点都在反比例函数图象上,可求得A、B两点的坐标;
(3)结合(1)、(2)中的坐标可猜得结论.
试题解析:(1)∵点A(1,3)在反比例函数y=![]() 上,∴k=3,
上,∴k=3,
∵点B(3,y2)在y=![]() 上,
上,
∴y2=1,即B点坐标为(3,1),
把A、B两点坐标代入直线y=ax+b,
可得![]() ,解得
,解得![]() ,∴直线AB的解析式为y=﹣x+4,
,∴直线AB的解析式为y=﹣x+4,
当y=0时,x=4,∴P点坐标为(4,0);
(2)如图,过A作AD∥x轴,交y轴于点D,则AD⊥y轴,
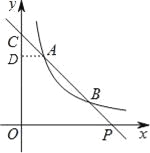
∴△ACD∽△PCO,∴![]() =
=![]() ,
,
∵b=y1+1,P(6,0),A(x1,y1),
∴CD=1,OC=y1+1,AD=x1,OP=6,
∴![]() =
=![]() ,
,
∵AB=BP,A(x1,y1),
∴B为AP中点,且P为(6,0),∴B点坐标为(![]() ,
, ![]() ),∵A、B两点都在y=
),∵A、B两点都在y=![]() 上,∴x1y1=
上,∴x1y1=![]()
![]() ,解得x1=2,∴
,解得x1=2,∴![]() =
=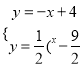 ,解得y1=2,∴A(2,2),B(4,1);
,解得y1=2,∴A(2,2),B(4,1);
(3)猜想x1,x2,x0之间的关系式为:x1+x2=x0.
理由如下:∵A(x1,y1),B(x2,y2),
∴![]() ,解得
,解得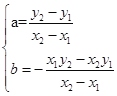 ,
,
∴直线AB解析式为y=![]() x﹣
x﹣![]() ,
,
令y=0可得x=![]() ,
,
∵x1y1=x2y2,
∴x=![]() =
=![]() =x1+x2,
=x1+x2,
即x1+x2=x0.


科目:初中数学 来源: 题型:
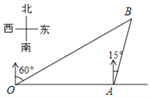
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A. 3![]() km B. 3
km B. 3![]() km C. 4km D. (3
km C. 4km D. (3![]() -3)km
-3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,B , C两点的坐标分别为 ![]() ,
, ![]() ,CD⊥y轴于点D , 直线l 经过点D.
,CD⊥y轴于点D , 直线l 经过点D.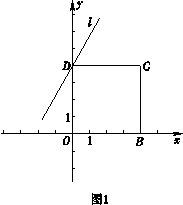
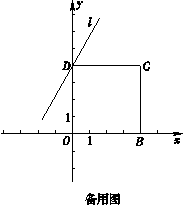
(1)直接写出点D的坐标;
(2)作CE⊥直线l于点E , 将直线CE绕点C逆时针旋转45°,交直线l于点F , 连接BF.
①依题意补全图形;
②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;
③通过思考、讨论,同学们形成了证明该猜想的几种思路:
思路1:作CM⊥CF , 交直线l于点M , 可证△CBF≌△CDM , 进而可以得出 ![]() ,从而证明结论.
,从而证明结论.
思路2:作BN⊥CE , 交直线CE于点N , 可证△BCN≌△CDE , 进而证明四边形BFEN为矩形,从而证明结论.
……
请你参考上面的思路完成证明过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程 ![]()
![]() 满足
满足 ![]() ,那么我们称这个方程为“阿凡达”方程,已知
,那么我们称这个方程为“阿凡达”方程,已知 ![]() 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2k+3)x+k2=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若两不相等的实数根满足![]() -
-![]() -
-![]() =-9,求实数k的值.
=-9,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com