
【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号 | 方程 | 方程的解 |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
… | … | … |
(1)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
(2)请写出这列方程中第n个方程:_____ 方程的解:_____.
【答案】12, 5, ![]() , x1=2n+2,x2=2n+2.
, x1=2n+2,x2=2n+2.
【解析】
首先根据已知方程两个重要数字、方程的解,找出与方程序号之间的关系,写出第n个方程,即可同时求出(1)、(2)两个问题答案.
(1)根据已知方程序号、方程两个重要数字、方程的解发现以下规律:
序号1,6=2×1+4 2=1+1 3=1+2 4=2×1+2;
序号2,8=2×2+4 3=2+1 4=2+2 6=2×2+2;
序号3,10=2×3+4 4=3+1 5=2+2 8=2×3+2;
序号4,12=2×4+4 5=4+1 6=4+2 10=2×4+2;
由序号4可以发现方程![]() (a>b)解x1=6,x2=10,
(a>b)解x1=6,x2=10,
12=2×4+4 5=4+1,
∴a=12,b=5.
故答案为:12,5.
(2)由(1)分析得:
序号n,2n+4=2×n+4 n+1=n+1 n+2=n+2 2n+2=2×n+2;
∴这列方程中第n个方程:![]() ,且方程的解为:x1=n+2,x2=2n+2.
,且方程的解为:x1=n+2,x2=2n+2.
故答案为:![]() ,x1=n+2,x2=2n+2.
,x1=n+2,x2=2n+2.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.

查看答案和解析>>
科目:初中数学 来源: 题型:
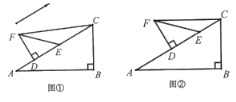
【题目】小刘同学在一次课外活动中,用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .图①是小刘同学所做的一个数学探究:他将
.图①是小刘同学所做的一个数学探究:他将![]() 的直角边
的直角边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() 、
、![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).
重合).
(1)在![]() 沿
沿![]() 方向移动的过程中,小刘发现:
方向移动的过程中,小刘发现:![]() 、
、![]() 两点间的距离逐渐 ;连接
两点间的距离逐渐 ;连接![]() 后,
后,![]() 的度数逐渐 .(填“不变”、“变大”或“变小”);
的度数逐渐 .(填“不变”、“变大”或“变小”);
(2)小刘同学经过进一步地研究,编制了如下问题:
问题①:如图②,当![]() 、
、![]() 的连线与
的连线与![]() 平行时,求平移距离
平行时,求平移距离![]() 的长;
的长;
问题②:如图③,在![]() 的移动过程中,
的移动过程中,![]() 的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.
的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
(1)![]() ________;
________;![]() ________;并求直线
________;并求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:任意两个数a,b,按规则c=![]() a+b得到一个新数c,称所得的新数c为数a,b的“传承数。”
a+b得到一个新数c,称所得的新数c为数a,b的“传承数。”
(1)若a=1,b=2,求a,b的“传承数”c;
(2)若a=1,b=![]() ,且
,且![]() +3x+1=0,求a,b的“传承数”c;
+3x+1=0,求a,b的“传承数”c;
(3)若a=2n+1,b=n1,且a,b的“传承数”c值为一个整数,则整数n的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2 个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢,赢的一方得电影票.
(1)游戏规则1:两人各摸1个球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
(2)游戏规则2; 两人同时各摸1个球,若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏小明赢得电影票的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD.(S表示面积)
实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+![]() .
.
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF=![]() ,求EG的长.
,求EG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com