
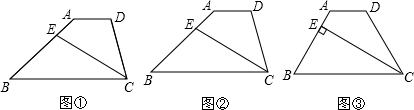
如图(1)四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
(1)用序号写出一个真命题(书写形式如:如果×××,那么××),并给出证明;
(2)用序号再写出三个真命题(不要求证明);
(3)加分题:真命题不止以上四个,想一想,就能够多写出几个真命题,每多写出一个真命题就给你加1分,最多加2分.

|
解答:(1)1)如果①②③,那么④⑤ 理由如下:如图(2),延长AE交BC的延长线于F ∵AD∥BC∴∠1=∠F 又∵∠AED=∠CEF,DE=EC ∴△ADE≌△FCE ∴AD=CFAE=EF ∵∠1=∠F,∠1=∠2, ∴∠2=∠F ∴AB=BF∴∠3=∠4 ∴AD+BC=CF+BC=BF=AB
2)如果①②④,那么③⑤ 理由如下:延长BC交AE的延长线于F,其证明方法与上类似, 略. 3)如果①②⑤,那么③④ 理由如下:如图(2),延长AE交BC的延长线于F 由AD∥BC,DE=CE.可证△ADE≌△FCE. ∴AD=CF,AE=EF ∵AD+BC=AB∴AB=FB ∴∠2=∠F=∠1,∠3=∠4 4)如果①③④,那么②⑤ 理由如下:方法一:仍如图(2),延长AE交BC的延长线于F ∵AD∥BC∴∠1=∠F ∵∠1=∠2∴∠2=∠F 又∠3=∠4,BE=BE∴△ABE≌△FBE ∴AE=FE,AB=FB ∴△ADE≌△FCE ∴AD=FC,DE=CE.从而AD+BC=AB 此外,本命题也可以这样证明. |


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
| AE | BE |
查看答案和解析>>
科目:初中数学 来源: 题型:
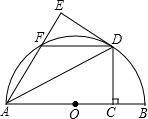 叠得到△AED,AE交半圆于点F,连接DF.
叠得到△AED,AE交半圆于点F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
(2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为 | BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 E=AD=AF=EF,⊙O 的半径为1.
E=AD=AF=EF,⊙O 的半径为1.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•下城区二模)如图,AB是半圆O的直径,且AB=4
(2013•下城区二模)如图,AB是半圆O的直径,且AB=4| 5 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com